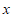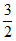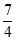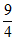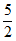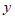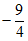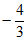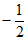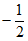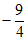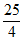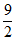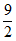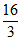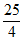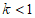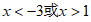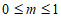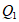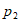本试卷共三道大题,28道小题。满分100分。考试时间120分钟。
一、选择题:(本大题共10小题,每题2分,共20分)
1. 下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的有( )
A. 1个 B. 2个 C. 3个 D. 4个
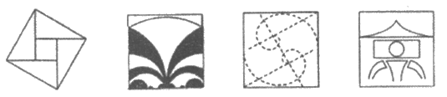
2. 若点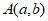 在双曲线
在双曲线 上,则代数式
上,则代数式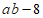 的值为( )
的值为( )
A. -12 B. -7 C. -5 D. 5
3. 关于方程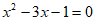 的根的情况,下列说法正确的是( )
的根的情况,下列说法正确的是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 无法判断
4. 如图,AC与BD相交于点E,AD∥BC,若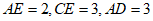 ,则BC的长度是( )
,则BC的长度是( )
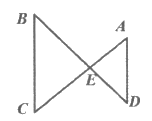
A. 2 B. 3 C. 4 D.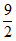
5. 如图,AB是⊙O的直径,点C、D在⊙O上,且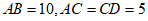 ,则∠ABD的度数为( )
,则∠ABD的度数为( )
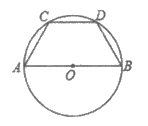
A. 30° B. 45° C. 50° D. 60°
6. 已知⊙O的半径是4,点P到圆心O的距离d为方程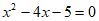 的一个根,则点P在( )
的一个根,则点P在( )
A. ⊙O的外部 B. ⊙O的内部
C. ⊙O上或⊙O的外部 D. ⊙O上或⊙O的内部
7. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=4,则线段AP的长为( )
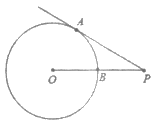
A. 4 B. 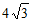 C. 8 D. 12
C. 8 D. 12
8. 如图,用一个半径为10cm的定滑轮带动重物上升,滑轮上一点P旋转了36°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
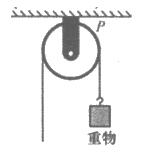
A. 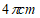 B.
B. 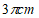 C.
C. 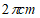 D.
D.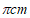
9. 如图,等腰直角三角形ABC中,∠ABC=90°,BA=BC,将BC绕点B顺时针旋转θ(0°<θ<90°),得到BP,连接CP,过点A作AH⊥CP交CP的延长线于点H,连接AP,则随着θ的增大,∠PAH的度数( )
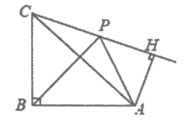
A. 增大 B. 减小 C. 不变 D. 先增大后减小
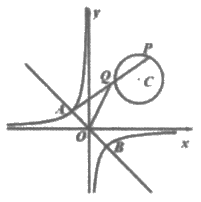
10. 如图,在平面直角坐标系中,直线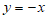 与双曲线
与双曲线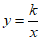 交于A,B两点,P是以点
交于A,B两点,P是以点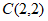 为圆心,半径长为1的圆上一动点,连接AP,Q为AP的中点,若线段OQ长度的最大值为2,则k的值为( )
为圆心,半径长为1的圆上一动点,连接AP,Q为AP的中点,若线段OQ长度的最大值为2,则k的值为( )
A. 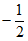 B.
B. 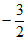 C. -2 D.
C. -2 D.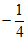
二、填空题:(本大题共10小题,每题3分,共30分)
11. 若关于x的方程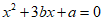 有一个根为-1,则
有一个根为-1,则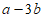 的值为__________。
的值为__________。
12. 已知反比例函数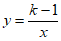 的图象分别位于第二、第四象限,请写出一个符合题意的k的值_______________。
的图象分别位于第二、第四象限,请写出一个符合题意的k的值_______________。
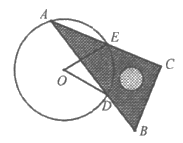
13. 如图,一块含30°角的直角三角板,将它的30°角顶点A落在⊙O上,边AB、AC分别与⊙O交于点D、E,则∠DOE的度数为___________。
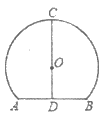
14. 石拱桥是中国传统桥梁四大基本形式之一,如图,已知一石拱桥的桥顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB=_________m。

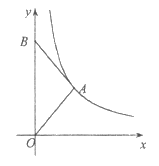
15. 如图,在平面直角坐标系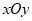 中,点B在y轴上,
中,点B在y轴上,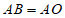 ,反比例函数
,反比例函数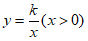 的图象经过点A,若△ABO的面积为2,则k的值为__________。
的图象经过点A,若△ABO的面积为2,则k的值为__________。
16. 一个圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面圆的半径为__________。
17. 已知抛物线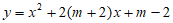 与x轴交于A、B(A在B左侧)两点,且对称轴为
与x轴交于A、B(A在B左侧)两点,且对称轴为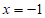 ,则(1)m的值为_________;(2)当
,则(1)m的值为_________;(2)当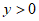 时,x的取值范围是_________。
时,x的取值范围是_________。
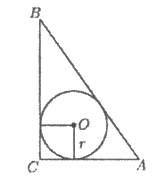
18. 如图,直角△ABC中,∠C=90°,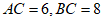 ,则△ABC的内切圆半径为_________。
,则△ABC的内切圆半径为_________。
19. 在平面直角坐标系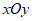 中,函数
中,函数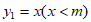 的图象与函数
的图象与函数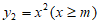 的图象组成图形G,对于任意实数n,过点
的图象组成图形G,对于任意实数n,过点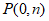 且与x轴平行的直线总与图形G有公共点,则实数m的取值范围是_______________。
且与x轴平行的直线总与图形G有公共点,则实数m的取值范围是_______________。
20. 三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3。
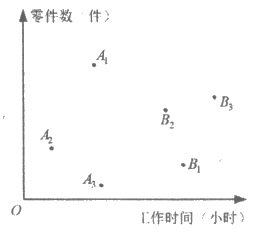
(1)记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是___________;
(2)记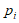 为第i名工人在这一天中平均每小时加工的零件数,则
为第i名工人在这一天中平均每小时加工的零件数,则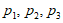 中最大的是________________。
中最大的是________________。
三、解答题(本题共50分,第21题6分,第22~23题,每小题5分;第24~25题,每小题6分;第26~27题,每小题7分,第28题8分)
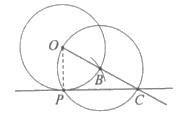
21. 下面是小美设计的”过圆上一点作圆的切线”的尺规作图过程。
已知:如图,⊙O及⊙O上一点P。
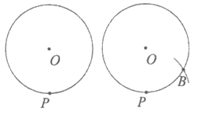
求作:过点P的⊙O的切线。
作法:如图,
①以点P为圆心,以OP为半径画弧交⊙O于点B;
②以点B为圆心,OB为半径作⊙B;
③连接OB并延长与⊙B交于另一点C;
④作直线PC;
则直线PC即为所求。
根据小美设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:连接OP,
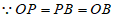 ,∴点P在⊙B上,
,∴点P在⊙B上,
又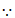 OC是⊙B的直径,∴∠OPC=90°(________________)(填推理的依据)。
OC是⊙B的直径,∴∠OPC=90°(________________)(填推理的依据)。
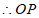 ⊥PC于点P,
⊥PC于点P,
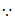 点P在⊙O上,
点P在⊙O上,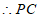 是⊙O的切线(_______________)(填推理的依据)。
是⊙O的切线(_______________)(填推理的依据)。
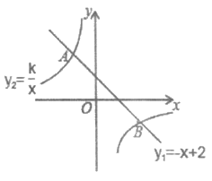
22. 如图,一次函数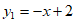 的图象与反比例函数
的图象与反比例函数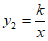 的图象相交于A,B两点,点B的坐标为
的图象相交于A,B两点,点B的坐标为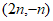 。
。
(1)求出n的值,并确定反比例函数的表达式;
(2)请直接写出当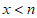 时,
时,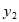 的取值范围。
的取值范围。
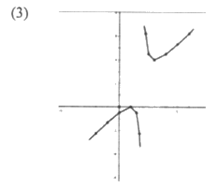
23. 有这样一个问题:探究函数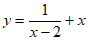 的图象与性质。
的图象与性质。
小亮根据学习函数的经验,对函数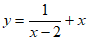 的图象与性质进行了探究。
的图象与性质进行了探究。
下面是小亮的探究过程,请补充完整:
(1)函数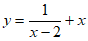 中自变量x的取值范围是______________;
中自变量x的取值范围是______________;
(2)下表是y与x的几组对应值,请直接写出m的值______________;
| … | -2 | -1 | 0 | 1 |
|
|
|
| 3 | 4 | 5 | 6 | … | |
| … |
|
|
| 0 |
|
|
|
| m |
|
|
| … | |
(3)在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
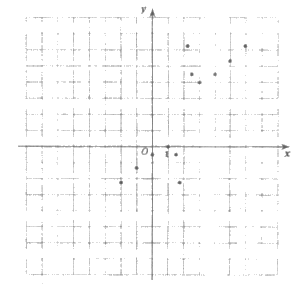
(4)根据画出的函数图象,发现下列特征:
①该函数的图象是中心对称图形,对称中心的坐标是_______________;
②该函数的图象与直线x=2越来越靠近而永不相交,该函数的图象还与直线_____________越来越靠近而永不相交。
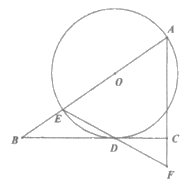
24. 如图,已知直角△ABC中,∠ACB=90°,E为AB上一点,以AE为直径作⊙O与BC相切于点D,连接ED并延长交AC的延长线于点F。
(1)求证: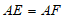 ;
;
(2)若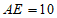 ,
,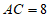 ,求BE的长。
,求BE的长。
25. 中国女排在历次比赛中都取得了优异成绩,她们的训练场如图1所示,长为18m,宽为9m,网高为2.24m,某队员站在底线O点处发球,球从点O的正上方1.9m的点C发出,运动路线是抛物线的一部分,当球运动到最高点A时,高度为2.88m,即BA=2.88m,这时水平距离OB=7m,以直线OB为x轴,直线OC为y轴,建立平面直角坐标系,如图2。
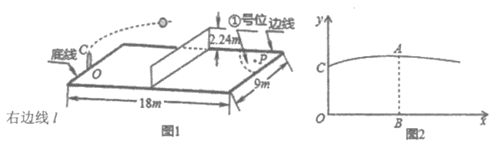
(1)若球向正前方运动(即x轴垂直于底线),求球运动的高度y(m)与水平距离x(m)之间的函数关系式(不必写出x取值范围),并判断这次发球能否过网?是否出界?说明理由。
(2)若球过网后的落点是对方场地①号位内的点P(如图1,点P距底线1m,左边线0.5m),求发球点O到右边线所在直线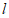 的距离。(参考数据:
的距离。(参考数据: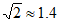 )
)
26. 已知二次函数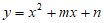 的图象经过点
的图象经过点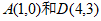 ,与x轴的另一个交点为B,与y轴交于点C。
,与x轴的另一个交点为B,与y轴交于点C。
(1)求二次函数的表达式及顶点坐标;
(2)将二次函数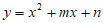 的图象在点B、C之间的部分(包含点B、C)记为图象G。已知直线
的图象在点B、C之间的部分(包含点B、C)记为图象G。已知直线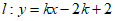 总位于图象G的上方,请直接写出k的取值范围:_____________。
总位于图象G的上方,请直接写出k的取值范围:_____________。
(3)如果点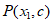 和点
和点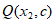 在函数
在函数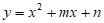 的图象上,且
的图象上,且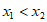 ,
,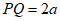 ,求
,求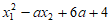 的值。
的值。
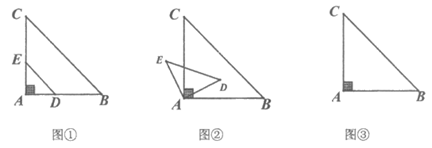
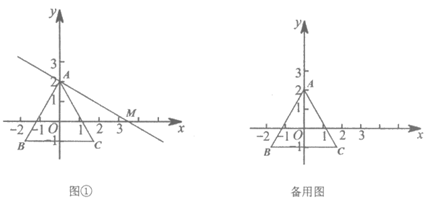
27. 如图①,在等腰直角△ABC中,∠A=90°,AB=AC=3,在边AB上取一点D(点D不与点A,B重合),在边AC上取一点E,使AE=AD,连接DE. 把△ADE绕点A逆时针方向旋转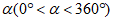 ,如图②。
,如图②。
(1)请你在图②中,连接CE和BD,判断线段CE和BD的数量关系,并说明理由;
(2)请你在图③中,画出当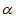 =45°时的图形,连接CE和BE,求出此时△CBE的面积;
=45°时的图形,连接CE和BE,求出此时△CBE的面积;
(3)若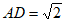 ,点M是CD的中点,在△ADE绕点A逆时针方向旋转的过程中,直接写出线段AM的最大值:_____________。
,点M是CD的中点,在△ADE绕点A逆时针方向旋转的过程中,直接写出线段AM的最大值:_____________。
28. 等边三角形的内切圆半径为r,外接圆半径为R,给出如下定义:设平面内一点到等边三角形中心的距离为d,满足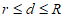 的点叫做等边三角形的”环中心点”。在平面直角坐标系
的点叫做等边三角形的”环中心点”。在平面直角坐标系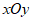 中,等边△ABC的三个顶点的坐标分别为
中,等边△ABC的三个顶点的坐标分别为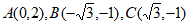 。
。
(1)已知点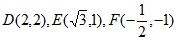 ,在点D、E、F中,是等边△ABC的”环中心点”的是:________________;
,在点D、E、F中,是等边△ABC的”环中心点”的是:________________;
(2)如图,
①过点A作直线交x轴正半轴于点M,使∠AMO=30°,若线段AM上存在等边△ABC的”环中心点”P(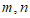 ),求m的取值范围;
),求m的取值范围;
②与①中AM平行的直线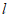 与x轴、y轴分别交于点
与x轴、y轴分别交于点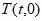 、
、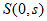 ,请直接写出:当s满足什么条件时,线段TS上总存在等边△ABC的”环中心点”:___________________。
,请直接写出:当s满足什么条件时,线段TS上总存在等边△ABC的”环中心点”:___________________。
【试题答案】
一、选择题(本题共20,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | B | C | A | D | D | A | B | C | C | A |
二、填空题(本题共30,每小题3分)
题号 | 11 | 12 | 13 | 14 | 15 | ||
答案 | -1 |
| 60° | 8 | 2 | ||
题号 | 16 | 17 | 18 | 19 | 20 | ||
答案 | 6 | -1 |
| 2 |
|
|
|
三、解答题(本题共50,第21题6分,第22~23题,每小题5分;第24~25题,每小题6分;第26~27题,每小题7分,第28题8分)解答应写出文字说明、验算步骤或证明过程。
21. (本小题满分6分)
补全的图形如图所示
 2分
2分
直径所对的圆周角是直角 4分
经过半径的外端且垂直于这条半径的直线是圆的切线 6分
22. (本小题满分5分)
(1)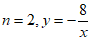 3分
3分
(2)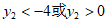 5分
5分
23. (本小题满分5分)
(1)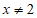 1分
1分
(2)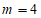 2分
2分
 3分
3分
(4)(2,2) 4分
(5) 5分
5分
24. (本小题满分6分)
证明:(1)连接OD
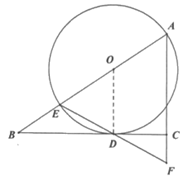
∵BC切⊙O于点D
∴OD⊥BC 1分
∴∠ODC=90°
又∵∠ACB=90°
∴OD∥AC
∴∠ODE=∠F 2分
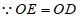
∴∠OED=∠ODE
∴∠OED=∠F
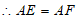 3分
3分
(2)∵OD∥AC
∴△BOD∽△BAC 4分
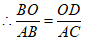
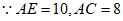
即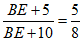 5分
5分
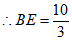 6分
6分
(本题方法多样)
25. (本小题满分6分)
(1)设抛物线的表达式为: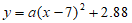 ,
,
将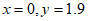 代入上式并解得:
代入上式并解得: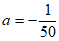 ,
,
故抛物线的表达式为: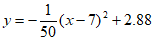 , 2分
, 2分
当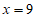 时,
时,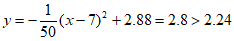 , 3分
, 3分
当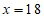 时,
时,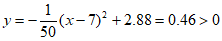 , 4分
, 4分
故这次发球过网,但是出界了。
(2)如图,分别过点作底线、边线的平行线PQ,OQ交于点Q,
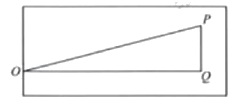
在Rt△OPQ中,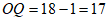 ,
,
当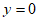 时,
时,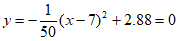 ,解得:
,解得: 或-5(-5舍去),
或-5(-5舍去),
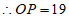 ,而
,而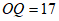 ,
,
故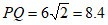 ,
,
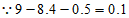 ,
,
∴发球点O在底线上且距右边线0.1米处。 6分
26. (本小题满分7分)
(1)根据题意得: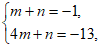 解得
解得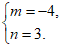
二次函数的表达式为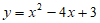 , 1分
, 1分
顶点坐标为(2,-1)。 2分
(2)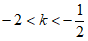 4分
4分
(3)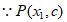 和点
和点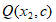 在函数
在函数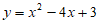 的图像上,
的图像上,
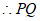 ∥x轴, 5分
∥x轴, 5分
又∵二次函数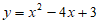 的对称轴是直线
的对称轴是直线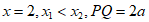 ,
,
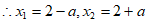 , 6分
, 6分
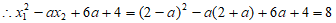 。 7分
。 7分
法2: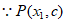 和点
和点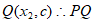 ∥x轴, 5分
∥x轴, 5分
又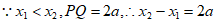 ①
①
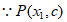 和点
和点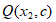 在函数
在函数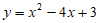 的图像上,
的图像上,
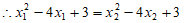 ,整理得
,整理得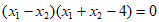
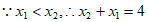 ②
②
由①②得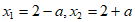 。 6分
。 6分
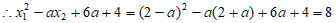 。 7分
。 7分
27.(本小题满分7分)
(1)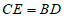 ; 1分
; 1分
理由:连接CE和BD,如图2所示,
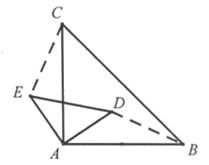
图2
由题意可知,△ABC和△ADE都是等腰直角三角形,
∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB,
又∵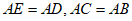 ,
,
∴△AEC≌△ADB(SAS),
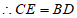 。 2分
。 2分
(2)当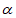 =45°时,连接CE和BE,如图3所示,延长AD交BC于F, 3分
=45°时,连接CE和BE,如图3所示,延长AD交BC于F, 3分
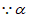 =45°,△ABC和△ADE都是等腰直角三角形,
=45°,△ABC和△ADE都是等腰直角三角形,
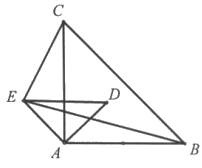
图3
∴∠BAF=∠CAF=∠EAC=45°,
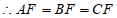 ,∠EAB=135°,
,∠EAB=135°,
∴∠EAB+∠ABC=135°+45°=180°,
∴AE∥BC, 4分
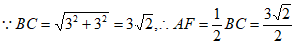 ,
,
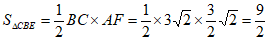 。 5分
。 5分
(3)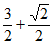 7分
7分
28. (本小题满分8分)
(1)E,F。 2分
(2)①依题意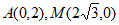 ,
,
可求得直线AM的解析式为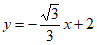 。 3分
。 3分
经验证E在直线AM。
因为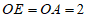 ,∠MAO=60°,
,∠MAO=60°,
所以△OAE为等边三角形,
所以AE边上的高长为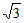 。 4分
。 4分
当点P在AE上时,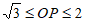 ,
,
所以当点P在AE上时,点P都是等边△ABC的环中心点,
所以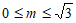 。 5分
。 5分
②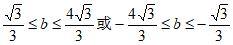 。 8分
。 8分