一、选择题(本题共30分,每小题3分)
第1-10题均有四个选项,符合题意的选项只有一个。
1. 下列图案中,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D.
2. 一元二次方程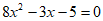 的二次项系数、一次项系数、常数项分别是( )
的二次项系数、一次项系数、常数项分别是( )
A. 8,-3,-5 B. 8,3,5 C. 8,3,-5 D. 8,-3,5
3. 下列函数中是二次函数的是( )
A. 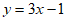 B.
B.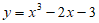
C. 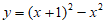 D.
D.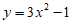
4. 抛物线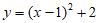 的顶点坐标为( )
的顶点坐标为( )
A. (-1,2) B. (1,2) C. (1,-2) D. (2,1)
5. 将抛物线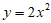 向下平移3个单位,得到的抛物线为( )
向下平移3个单位,得到的抛物线为( )
A. 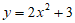 B.
B.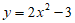
C. 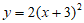 D.
D.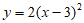
6. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A’B’C’,连接AA’,若∠1=25°,则∠BAC的度数是( )
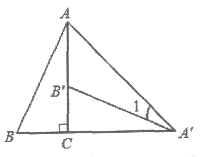
A. 10° B. 20° C. 30° D. 40°
7. 若关于x的一元二次方程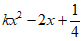 =0有实数根,则实数k的取值范围是( )
=0有实数根,则实数k的取值范围是( )
A. k<4 B. k<4且k≠0 C. k≤4 D. k≤4且k≠0
8. 如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数。若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )
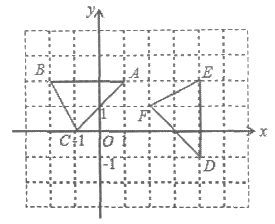
A. (0,0) B. (1,0) C. (1,-1) D. (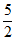 ,
,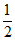 )
)
9. 如图,在平面直角坐标系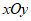 中,有五个点A(2,0),B(0,-2),C(-2,4),D(4,-2),E(7,0),将二次函数
中,有五个点A(2,0),B(0,-2),C(-2,4),D(4,-2),E(7,0),将二次函数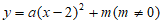 的图象记为W。下列的判断中
的图象记为W。下列的判断中
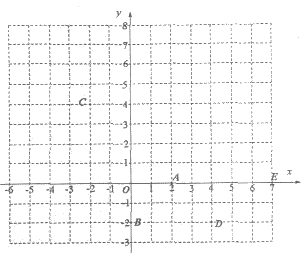
①点A一定不在W上;
②点B,C,D可以同时在W上;
③点C,E不可能同时在W上。
所有正确结论的序号是( )
A. ①②③ B. ①② C. ①③ D. ②③
10. 如图,正△ABC的边长为3 cm,动点P从点A出发,以每秒1 cm的速度,沿A→B→C的方向运动,到达点C时停止,设运动时间为x(秒),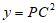 ,则y关于x的函数的图象大致为( )
,则y关于x的函数的图象大致为( )
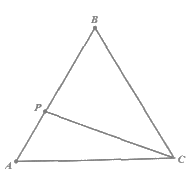
A. 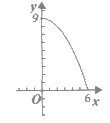 B.
B. 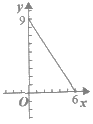 C.
C. 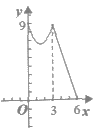 D.
D.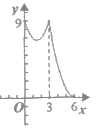
二、填空题(本题共16分,每小题2分)
11. 在平面直角坐标系xOy中,将点(-2,3)绕原点O旋转180°,所得到的对应点的坐标为_________。
12. 若二次函数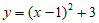 的图象上有两点A(0,a),B(5,b),则a_________b。(填”>”,”=”或”<“)
的图象上有两点A(0,a),B(5,b),则a_________b。(填”>”,”=”或”<“)
13. 商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是_________。
14. 已知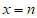 是关于x的一元二次方程
是关于x的一元二次方程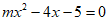 的一个根,若
的一个根,若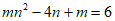 ,则m的值为_________。
,则m的值为_________。
15. 关于x的一元二次方程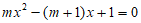 有两个不等的整数根,m为整数,那么m的值是_________。
有两个不等的整数根,m为整数,那么m的值是_________。
16. 已知二次函数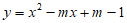 的图象与x轴只有一个公共点。
的图象与x轴只有一个公共点。
(1)求m=_________。
(2)当0≤x≤3时,y的取值范围为_________。
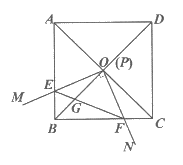
17. 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O。直角∠MPN的顶点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针绕点P旋转∠MPN,旋转角为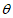 (0°<
(0°<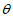 <90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论中正确的是_________。
<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论中正确的是_________。
①EF=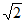 OE;
OE;
②记四边形OEBF的面积为S1,正方形ABCD的面积为S2,则S1:S2=1:4;
③BE+BF=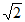 OA;
OA;
④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=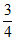 。
。
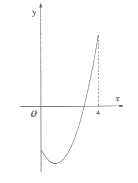
18. 函数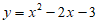 (0≤x≤4)的图象如下图,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象。若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是_________。
(0≤x≤4)的图象如下图,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象。若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是_________。
三、解答题(本题共54分,第19~25题,每小题5分,第26~27题,每小题6分,第28题7分)解答应写出文字说明、演算步骤或证明过程
19. 计算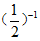 +|
+|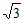 -2|+(3-
-2|+(3-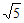 )0+(-2)2。
)0+(-2)2。
20. 解一元二次方程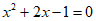 。
。
21. 对于抛物线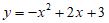 。
。
(1)抛物线与x轴的交点坐标是_________,顶点坐标是_________;
(2)在坐标系中画出此抛物线;
(3)结合图象回答,若y>0,则x的取值范围是_________.
22. 如图,已知等边三角形ABC,O为△ABC内一点,连接OA,OB,OC,将△BAO绕点B顺时针旋转至△BCM。
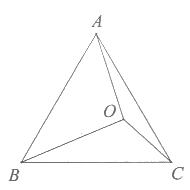
(1)依题意补全图形;
(2)若OA=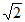 ,OB=
,OB=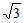 ,OC=1,求∠OCM度数。
,OC=1,求∠OCM度数。
23. 如图,直线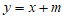 和抛物线
和抛物线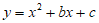 都经过点A(1,0),B(3,2)。
都经过点A(1,0),B(3,2)。
(1)求m的值和抛物线的解析式;
(2)结合函数图象,求关于x的不等式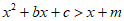 的解集。(直接写出答案)
的解集。(直接写出答案)
24. 在”新冠”疫情期间,全国人民”众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫。已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售。调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:
x(元/件) | 12 | 13 | 14 | 15 | 16 |
y(件) | 1200 | 1100 | 1000 | 900 | 800 |
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件。试问:当x为多少时,线上和线下利润总和达到最大?并求出此时的最大利润。
25. 探究函数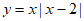 的图象与性质。
的图象与性质。
小娜根据学习函数的经验,对函数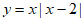 的图象与性质进行了探究。下面是小娜的探究过程,请补充完整:
的图象与性质进行了探究。下面是小娜的探究过程,请补充完整:
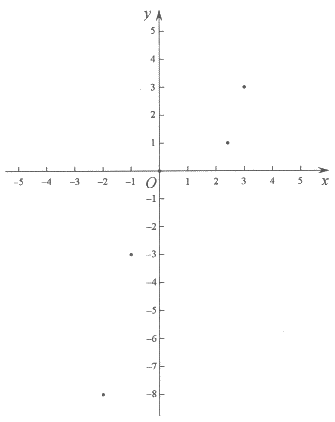
(1)下表是x与y的几组对应值。
x | … | -2 | -1 | 0 | 1 | 2 | 1+ | 3 | … |
y | … | -8 | -3 | 0 | m | n | 1 | 3 | … |
请直接写出:m=_______,n=_______;
(2)如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;
(3)结合画出的函数图象,解决问题:若方程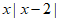 =a有三个不同的解,记为x1,x2,x3,且x1< x2< x3请直接写出x1+ x2+ x3的取值范围。
=a有三个不同的解,记为x1,x2,x3,且x1< x2< x3请直接写出x1+ x2+ x3的取值范围。
26. 在平面直角坐标系xOy中,二次函数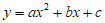 的图象经过点A(0,-4)和B(-2,2)。
的图象经过点A(0,-4)和B(-2,2)。
(1)求c的值,并用含a的式子表示b;
(2)当-2<x<0时,若二次函数满足y随x的增大而减小,求a的取值范围;
(3)直线AB上有一点C(m,5),将点C向右平移4个单位长度,得到点D。若抛物线与线段CD只有一个公共点,直接写出a的取值范围________。
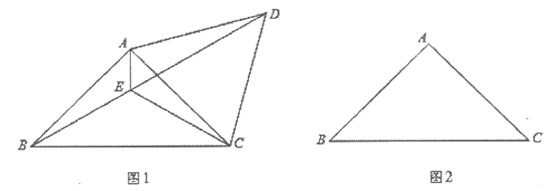
27. 已知:在△ABC中,∠BAC=90°,AB=AC。
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连接CD、BD,∠BAC平分线交BD于点E,连接CE。
①用等式表示线段BD、AE、EC之间的数量关系(直接写出结果);
②求证:∠AED=∠CED;
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连接CD,BD,∠BAC的平分线BD的延长线于点E,连接CE。请补全图形,用等式表示线段AE,CE,BD之间的数量关系,并证明。
28. 我们定义:对于抛物线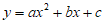 (a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M成中心对称的抛物线y‘,则我们称抛物线y‘为抛物线y的”衍生抛物线”,点M为”衍生中心”。
(a≠0),以y轴上的点M(0,m)为中心,作该抛物线关于点M成中心对称的抛物线y‘,则我们称抛物线y‘为抛物线y的”衍生抛物线”,点M为”衍生中心”。
(1)已知抛物线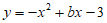 经过点(-1,0),则b=_______,顶点坐标为_______,该抛物线关于点(0,1)成中心对称的抛物线的表达式是_______;
经过点(-1,0),则b=_______,顶点坐标为_______,该抛物线关于点(0,1)成中心对称的抛物线的表达式是_______;
(2)已知抛物线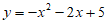 关于点(0,m)的衍生抛物线为y‘,若这两条抛物线有交点,求m的取值范围;
关于点(0,m)的衍生抛物线为y‘,若这两条抛物线有交点,求m的取值范围;
(3)已知抛物线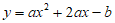 (a≠0)。若抛物线y关于点(0,k+12)的衍生抛物线为y1,其顶点为A1;关于点(0,k+22)的衍生抛物线为y2,其顶点为A2;…;关于点(0,k+n2)的衍生抛物线为yn,其顶点为An;…(n为正整数),直接写出AnAn+1的长_________(用含n的式子表示)。
(a≠0)。若抛物线y关于点(0,k+12)的衍生抛物线为y1,其顶点为A1;关于点(0,k+22)的衍生抛物线为y2,其顶点为A2;…;关于点(0,k+n2)的衍生抛物线为yn,其顶点为An;…(n为正整数),直接写出AnAn+1的长_________(用含n的式子表示)。
参考答案
一、选择题(本题共30分,每小题3分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | A | D | B | B | B | D | C | B | D |
二、填空题(本题共16分,每小题2分)
11. (2,-3) 12. < 13. 50%
14. 1 15. -1
16. (1)2 (2)0≤y≤4 17. ①②③
18. 0≤m≤1
三、解答题(本题共54分,第19~25题,每小题5分,第26~27题,每小题6分,第28题7分)解答应写出文字说明、演算步骤或证明过程。
19. (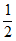 )-1+|
)-1+|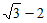 |+(3-
|+(3-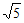 )0+(-2)2
)0+(-2)2
=2+2-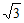 +1+4 …. . . . . . . 4分
+1+4 …. . . . . . . 4分
=9-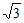 ……………5分
……………5分
20. 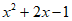
=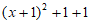
=x+1=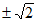 ……………3分
……………3分
=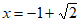 或
或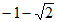 . . . . . . . . . . . . . . 5分
. . . . . . . . . . . . . . 5分
21. (1)(-1,0)和(3,0) 2分
(1,4) …3分
(2)图…4分
(3)-1<x<3 …5分
22. (1)图…1分
(2)作∠OBM=60°,使得BM=BO,连接OM,CM………2分
证明△ABO≌△CBM(SAS)········3分
所以CM=AO。因为△BOM是等边三角形,所以OM=OB。因为AO=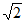 ,BO=
,BO=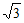 ,CO=1,所以OM=
,CO=1,所以OM=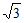 ,CM=
,CM=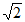 ………4分
………4分
所以OC2+CM2=OM2,所以△OCM是直角三角形。所以∠OCM=90°………5分
23. (1)把A(1,0),B(3,2)代入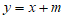 和
和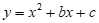 中
中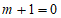 ,
,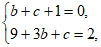 解得
解得
m=-1 1分
b=-3 2分
c=2 3分
所以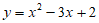 。
。
(2)x<1或x>3 ···5分
24. (1)设一次函数解析式为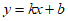 (k≠0)。(12,1200),(16,800)代入
(k≠0)。(12,1200),(16,800)代入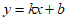 (k≠0)得
(k≠0)得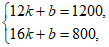 从而
从而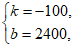 所以
所以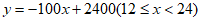 …2分
…2分
(2)设商家线上和线下利润总和为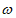 。
。
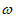 =400(x-10-2)+y(x-10) ······3分
=400(x-10-2)+y(x-10) ······3分
=-100(x-19)2+7300 ······4分
当x=19时,利润最大,为7300……5分。
25. (1)m=1 1分 n=0 2分
(2)图 …3分
(3)4<x1+ x2+ x3 <3+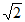 5分
5分
26. (1)把A(0,-4),B(-2,2)代入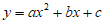 ,c=-4 1分
,c=-4 1分
4a-2b+c=2,故b=2a-3 2分
(2)当a>0时,依题意对称轴满足-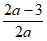 ≥0
≥0 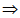 0<a≤
0<a≤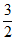 ;
;
当a<0时,依题意对称轴满足-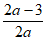 ≤-2
≤-2 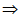 –
–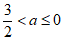 。
。
综上-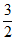 ≤a<0或0<a≤
≤a<0或0<a≤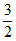 ……4分
……4分
(3)0<a<4或a=-3- ……6分
……6分
27.
证明:(1)
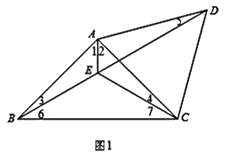
①BD=2CE+AE
理由如下:
过点A作AH⊥BD于点H,
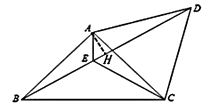
∵∠EBC=∠ECB
∴BE=CE,
∵∠AED=60°,AH⊥BD
∴AE=2EH
∵AB=AD,AH⊥BD
∴BD=2BH=2(BE+EH)
=2BE+AE=2EC+AE
②∵将线段AC绕点A逆时针旋转60°得到AD,
∴AC=AD,∠DAC=60°
∴∠BAD=∠BAC+∠CAD=150°,且AB=AC=AD
∴∠3=∠5=15°
∴∠BAC=90°,AB=AC,AE平分∠BAC
∴∠1=∠2=45°,∠ABC=∠ACB=45°
又∵AE=AE,
∴△ABE≌△ACE(SAS)
∴∠3=∠4=15°
∴∠6=∠7=30°
∴∠DEC=∠6+∠7=60°
∵∠AED=∠3+∠1=60°
∴∠AED=∠CED
(2)补全图形如图,
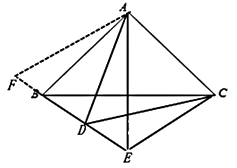
2CE-AE=BD
理由如下:
如图2,以A为顶点,AE为一边作∠EAF=60°,AF交DB延长线于点F。
∵∠BAC=90°,AB=AC,AE平分∠BAC
∴∠BAE=∠CAE=45°,
∠ABC=∠ACB=45°。
∵将线段AC绕点A逆时针旋转60°得到AD,
∴AC=AD, ∠DAC=60°
∴∠DAE=∠DAC-∠CAE=15°,AB=AD
∴∠ABD=∠ADB, ∠BAD=30°
∴∠ABD=∠ADB=75°
∴∠AED=∠ADB-∠DAE=60°
∵∠EAF=60°
又∵∠EAF=60°,
∴∠F=60°
∴△AEF是等边三角形。
∴AE=AF=EF。
∵AC=AD,∠CAE=∠DAF=45°,
AE=AF,
∴△CAE≌△DAF(SAS)。
∴CE=DF。
∵AB=AC, ∠BAE=∠CAE=45°,
AE=AE,
∴△BAE≌CAE(SAS)。
∴BE=CE。
∴BE=CE。
∵DF+BE-EF=BD,
∴2CE-AE=BD
28. (1)b=-4 (-2,1) 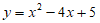 …3分
…3分
(2)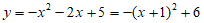 ,顶点坐标为(-1,6) ……4分
,顶点坐标为(-1,6) ……4分
(-1,6)关于(0,m)对称点为(1,2m-6)。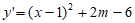 ,令
,令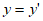 得
得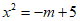 ,两条抛物线有交点,故-m+5≥0,m≤5 ……6分
,两条抛物线有交点,故-m+5≥0,m≤5 ……6分
(3)4n+2 ……7分