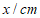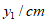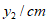(考试时间:120分钟 满分:100分)
一、选择题:本大题共16分,每题2分。
1. 中国国家航天局2020年4月24日在”中国航天日”之际宣布,将中国行星探测任务命名为”天问”,将中国首次火星探测任务命名为”天问一号”,火星具有与地球十分相近的环境,与地球最近的时候距离约5500万千米,将5500用科学记数法表示为
A. 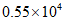 B.
B. 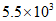 C.
C. 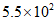 D.
D.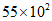
2. 若一个多边形的内角和是720°,则这个多边形的边数是
A. 5 B. 6 C. 7 D. 8
3. 实数a,b,c在数轴上的对应点的位置如图所示,则下列结论正确的是
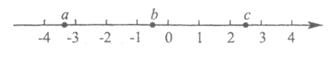
A. 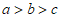 B.
B. 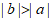 C.
C. 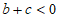 D.
D.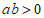
4. 如图,直线a∥b,直线l与a,b分别交于A,B两点,过点B作BC⊥AB交直线a于点C,若∠1=65°,则∠2的度数为
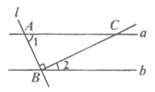
A. 25° B. 35° C. 65° D. 115°
5. 如果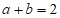 ,那么
,那么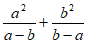 的值是
的值是
A. 2 B. 4 C. -2 D. -4
6. 把直线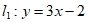 向右平移2个单位可以得到直线
向右平移2个单位可以得到直线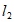 ,要得到直线
,要得到直线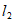 ,也可以把直线
,也可以把直线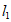
A. 向上平移2个单位 B. 向下平移2个单位
C. 向上平移6个单位 D. 向下平移6个单位
7. 在平面直角坐标系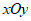 中,点P在由直线
中,点P在由直线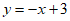 ,直线
,直线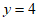 和直线
和直线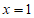 所围成的区域内或其边界上,点Q在x轴上,若点R的坐标为
所围成的区域内或其边界上,点Q在x轴上,若点R的坐标为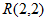 ,则
,则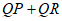 的最小值为
的最小值为
A. 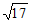 B.
B. 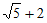 C.
C. 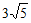 D. 4
D. 4
8. “实际平均续航里程”是指电动汽车的行驶总里程与充电次数的比值,是反映电动汽车性能的重要指标,厂家为了解某型号电动汽车的”实际平均续航里程”,收集了使用该型号电动汽车1年以上的部分客户的相关数据,按年龄不超过40岁和年龄在40岁以上将客户分为A,B两组,从A,B组各抽取10位客户的电动汽车的”实际平均续航里程”数据整理成下图,其中”⊙”表示A组的客户,”*”表示B组的客户。
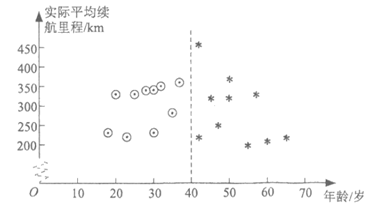
下列推断不正确的是
A. A组客户的电动汽车的”实际平均续航里程”的最大值低于B组
B. A组客户的电动汽车的”实际平均续航里程”的方差低于B组
C. A组客户的电动汽车的”实际平均续航里程”的平均值低于B组
D. 这20位客户的电动汽车的”实际平均续航里程”的中位数落在B组
二、填空题:本大题共16分,每题2分。
9. 若代数式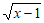 有意义,则实数x的取值范围是_________。
有意义,则实数x的取值范围是_________。
10. 分解因式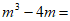 ____________。
____________。
11. 一次函数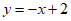 的图象不经过第___________象限。
的图象不经过第___________象限。
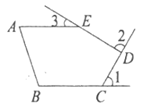
12. 如图,∠1,∠2,∠3均是五边形ABCDE的外角,AE∥BC,则∠1+∠2+∠3=________°。
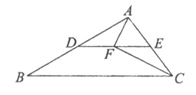
13. 如图,在△ABC中,∠ACB=50°,点D,E分别是AB,AC的中点,若点F在线段DE上,且∠AFC=90°,则∠FAE的度数为___________°。
14. 手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:
时间 模型 | 打磨(A组) | 组装(B组) |
模型1 | 9分钟 | 5分钟 |
模型2 | 6分钟 | 11分钟 |
则这两个模型都制作完成所需的最短时间为__________分钟。
15. 正方形ABCD的边长为4,点M,N在对角线AC上(可与点A,C重合),MN=2,点P,Q在正方形的边上,下面四个结论中,
①存在无数个四边形PMQN是平行四边形;②存在无数个四边形PMQN是菱形;
③存在无数个四边形PMQN是矩形;④至少存在一个四边形PMQN是正方形。
所有正确结论的序号是_______________。
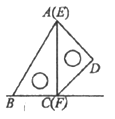
16. 如图所示,一副含30°和45°角的三角板ABC和EDF拼合在一个平面上,边AC与EF重合,AC=12cm,当点E从点A出发沿AC方向滑动时,点F同时从点C出发沿射线BC方向滑动,当点E从点A滑动到点C时,点D运动的路径长为____________cm。
三、解答题:本题共68分,第17—20题,每小题5分,21题6分,22题5分,第23—26题,每小题6分,第27题7分,28题6分
17. 计算: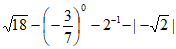 。
。
18. 解分式方程: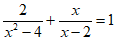 。
。
19. 下面是小星同学设计的”过直线外一点作已知直线的平行线”的尺规作图过程:

已知:如图,直线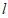 和直线
和直线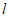 外一点A
外一点A
求作:直线AP,使得AP∥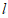
作法:如图
①在直线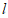 上任取一点B(AB与
上任取一点B(AB与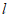 不垂直),以点A为圆心,AB为半径作圆,与直线
不垂直),以点A为圆心,AB为半径作圆,与直线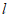 交于点C。
交于点C。
②连接AC,AB,延长BA到点D;
③作∠DAC的平分线AP。
所以直线AP就是所求作的直线
根据小星同学设计的尺规作图过程,
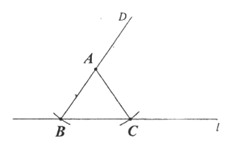
(1)使用直尺和圆规,补全图形(保留作图痕迹)
(2)完成下面的证明
证明:∵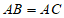 ,
,
∴∠ABC=∠ACB(___________)(填推理的依据)
∵∠DAC是△ABC的外角,
∴∠DAC=∠ABC+∠ACB(___________)(填推理的依据)
∴∠DAC=2∠ABC
∵AP平分∠DAC,
∴∠DAC=2∠DAP
∴∠DAP=∠ABC
∴AP∥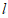 (____________)(填推理的依据)
(____________)(填推理的依据)
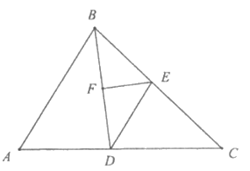
20. 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,F是BD中点。
求证:EF平分∠BED。
21. 已知关于x的方程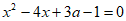 有两个实数根。
有两个实数根。
(1)求实数a的取值范围;
(2)若a为正整数,求方程的根。
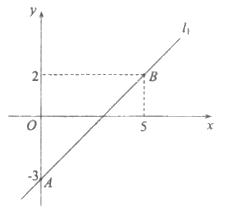
22. 在平面直角坐标系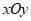 中,直线
中,直线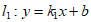 过
过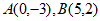 ,直线
,直线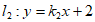 。
。
(1)求直线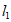 的表达式;
的表达式;
(2)当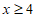 时,不等式
时,不等式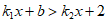 恒成立,请写出一个满足题意的
恒成立,请写出一个满足题意的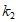 的值。
的值。
23. 如图,在△ABC中,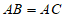 ,AD平分∠BAC,CE∥AD且
,AD平分∠BAC,CE∥AD且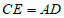 。
。
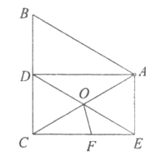
(1)求证:四边形ADCE是矩形;
(2)若△ABC是边长为4的等边三角形,对角线AC,DE相交于点O,在CE上截取CF=CO,连接OF,求四边形AOFE的面积。
24. 我国的传统佳节端午节,历来有吃”粽子”的习俗,某食品加工厂拥有A、B两条不同的粽子生产线,原计划A生产线每小时加工粽子400个,B生产线每小时加工粽子500个。
(1)若生产线A,B一共加工12小时,且生产粽子总数量不少于5500个,则B生产线至少加工多少小时?
(2)原计划A,B生产线每天均工作8小时,由于受其它原因影响,在实际生产过程中,A生产线每小时比原计划少生产100a个(a>0),B生产线每小时比原计划少生产100个,为了尽快将粽子投放到市场,A生产线每天比原计划多工作2a小时,B生产线每天比原计划多工作a小时,这样一天恰好生产粽子6400个,求a的值。
25. 如图,点P是AB上一动点,连接AP,作∠APC=45°,交弦AB于点C。已知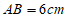 ,设
,设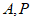 两点间的距离为
两点间的距离为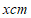 ,P,C两点间的距离为
,P,C两点间的距离为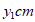 ,
,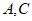 两点间的距离为
两点间的距离为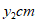 。(当点P与点A重合时,
。(当点P与点A重合时,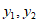 的值为0;当点P与点B重合时,
的值为0;当点P与点B重合时,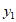 的值为0,
的值为0,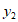 的值为6)。
的值为6)。
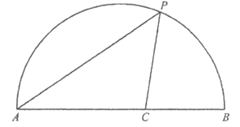
小元根据学习函数的经验,分别对函数y随自变量x的变化而变化的规律进行了探究。
下面是小元的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y与x的几组对应值;
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 0 | 1.21 | 2.09 | m | 2.99 | 2.82 | 0 |
| 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6 |
经测量m的值是__________(保留一位小数)。
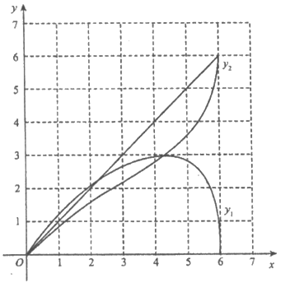
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;
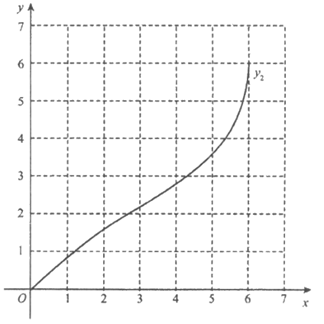
(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为___________cm(保留一位小数)。
26. 在平面直角坐标系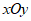 中,点
中,点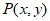 经过变换
经过变换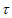 得到点
得到点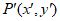 ,该变换记作
,该变换记作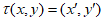 ,其中
,其中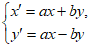 (
(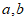 为常数)。
为常数)。
例如:当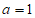 ,且
,且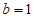 时,
时,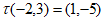 。
。
(1)当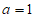 ,且
,且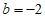 时,
时,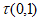 =_______;
=_______;
(2)若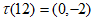 ,则a=__________,b=_________;
,则a=__________,b=_________;
(3)设点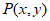 是直线
是直线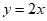 上的任意一点,点P经过变换
上的任意一点,点P经过变换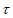 得到点
得到点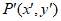 ,若点P与点
,若点P与点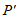 重合,求a和b的值。
重合,求a和b的值。
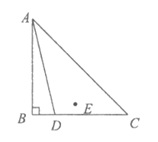
27. 已知:在△ABC中,∠ABC=90°,AB=BC,点D为线段BC上一动点(点D不与点B、C重合),点B关于直线AD的对称点为E,作射线DE,过点C作BC的垂线,交射线DE于点F,连接AE。
(1)依题意补全图形;
(2)AE与DF的位置关系是_____________;
(3)连接AF,点D在运动变化的过程中,∠DAF的度数是否始终保持不变,如果不变请求出其度数,如果变化请说明理由。
28. 在平面直角坐标系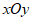 中,对任意两点
中,对任意两点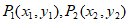 ,如果
,如果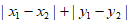 =d,则称
=d,则称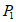 与
与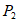 互为”
互为”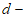 距点”。例如:点
距点”。例如:点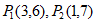 ,由
,由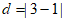 +
+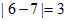 ,可得
,可得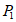 与
与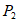 互为”3-距点”。
互为”3-距点”。
(1)在点D(-2,-2),E(5,-1),F(0,4)中,原点O的”4-距点”是__________(填字母);
(2)已知点A(2,1),点B(0,b),过点B平行于x轴的直线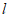 。
。
①当b=3时,直线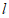 上的点A的”2-距点”的坐标为_____________________;
上的点A的”2-距点”的坐标为_____________________;
②若直线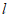 上存在点A的”2-距点”,在坐标系中画出这些A的”2-距点”组成的图形,并写出b的取值范围。
上存在点A的”2-距点”,在坐标系中画出这些A的”2-距点”组成的图形,并写出b的取值范围。
【试题答案】
一、选择题(本题共16分,每小题2分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | B | D | A | A | D | A | C |
二、填空题(本题共16分,每小题2分)
9. 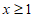 10.
10. 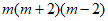 11. 三 12. 180
11. 三 12. 180
13. 64 14. 22 15. ①②④ 16.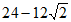
三、解答题(本题共68分,第17—20题,每小题5分,21题6分,22题5分,第23—26题,每小题6分,第27题7分,28题6分)
17. 解:原式=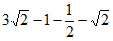 4分
4分
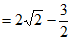 。 5分
。 5分
18. 解:方程两边同时乘以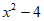 ,得
,得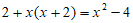 , 3分
, 3分
解得,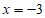 。 4分
。 4分
经检验,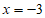 是原方程的解。 5分
是原方程的解。 5分
19. (1)略 2分
(2)等腰三角形两个底角相等(简写成:”等边对等角”) 3分
三角形的外角等于与它不相邻的两个内角和 4分
同位角相等,两直线平行 5分
20. 证明:∵BD平分∠ABC
∴∠ABD=∠CBD 1分
∵DE∥AB
∴∠ABD=∠BDE 2分
∴∠CBD=∠BDE 3分
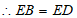 4分
4分
∵F是BD中点
∴EF平分∠BED 5分
21. 解:(1)∵关于x的方程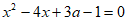 有两个实数根,
有两个实数根,
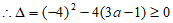 。 1分
。 1分
解得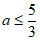 。 2分
。 2分
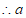 的取值范围为
的取值范围为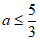 。
。
(2)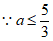 ,且a为正整数,
,且a为正整数,
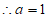 , 3分
, 3分
∴方程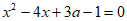 可化为
可化为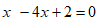 。 4分
。 4分
∴此方程的根为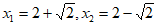 。 6分
。 6分
22. 解:(1)∵直线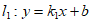 过
过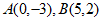 ,
,
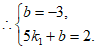 1分
1分
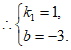 2分
2分
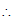 直线
直线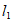 的表达式为
的表达式为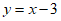 。 3分
。 3分
(2)答案不唯一,满足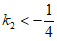 即可。 5分
即可。 5分
23. (1)证明:∵CE∥AD且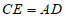 ,
,
∴四边形ADCE是平行四边形。 1分
又在△ABC中,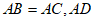 平分∠BAC,
平分∠BAC,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCE是矩形。 2分
(2)解:作OH⊥CE于点H,
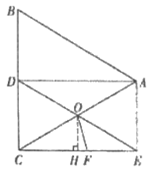
∵△ABC是边长为4的等边三角形,AD平分∠BAC,
∴∠BAC=60°,∠DAC=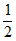 ∠BAC=30°,
∠BAC=30°,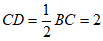 ,
,
由(1)知四边形ADCE是矩形,
∴AC与DE互相平分,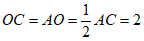 ,
,
∴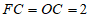 。 3分
。 3分
∵在矩形ABCD中,∠AEC=∠DCE=90°,
∴∠ACE=∠DAC=30°,
在Rt△COH中,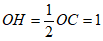 , 4分
, 4分
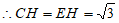 。
。
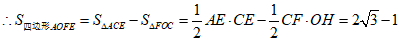 。 6分
。 6分
24.(1)解:设B生产线加工x小时,则A生产线加工(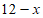 )小时。
)小时。
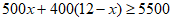 , 2分
, 2分
解得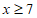 。 3分
。 3分
答:B生产线至少加工7小时。
(2)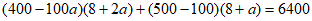 4分
4分
整理得,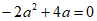 ,
,
解得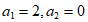 (不符合题意,舍去) 6分
(不符合题意,舍去) 6分
∴a的值为2
25. 解:(1)2.7; (±0.2) 1分
(2)如图; 3分
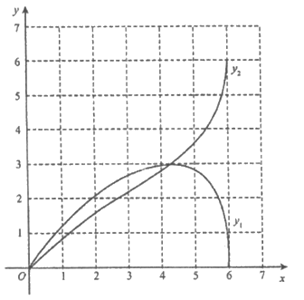
(3)2.3或4.2 6分
26. 解:(1)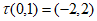 ; 1分
; 1分
(2)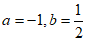 ; 3分
; 3分
(3)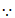 点
点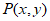 经过变换
经过变换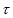 得到的对应点
得到的对应点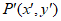 与点P重合,
与点P重合,
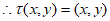 ,
,
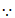 点
点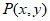 在直线
在直线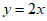 上,
上,
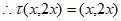 ,
,
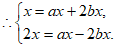 4分
4分
即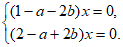
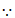 x为任意的实数,
x为任意的实数,
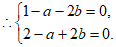 解得
解得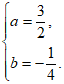
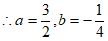 。 6分
。 6分
27. 解:(1)补全图形如下:
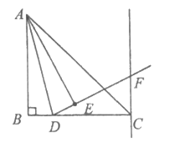 1分
1分
(2)AE与DF的位置关系是互相垂直; 2分
(3)∠DAF=45° 3分
(想法1图形)
证明如下:过点A做AG⊥CF于点G,依题意可知:
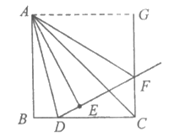
∠B=∠BCG=∠CGA=90°,
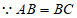 ,
,
∴四边形ABCG是正方形 4分
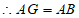 ,∠BAG=90°
,∠BAG=90°
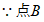 关于直线AD的对称点为E,
关于直线AD的对称点为E,
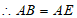 ,∠B=∠AED=90°,∠BAD=∠EAD。 5分
,∠B=∠AED=90°,∠BAD=∠EAD。 5分
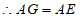
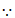
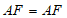 ,
,
∴Rt△AFG≌Rt△AFE(HL), 6分
∴∠GAF=∠EAF,
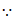 ∠BAG=90°,
∠BAG=90°,
∴∠BAD+∠EAD+∠EAF+∠GAF=90°,
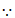 ∠BAD=∠EAD,∠EAF=∠GAF,
∠BAD=∠EAD,∠EAF=∠GAF,
∴∠EAD+∠EAF=45°,
即∠DAF=45°。 7分
(想法2图形)
证明如下:过点B作BG∥AF,交直线FC于点G,
依题意可知:∠ABC=∠BCF=90°
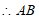 ∥FG
∥FG
 ∥BG
∥BG
∴四边形ABGF是平行四边形 4分
 ,∠BGC=∠BAF,
,∠BGC=∠BAF,
 点B关于直线AD的对称点为E。
点B关于直线AD的对称点为E。
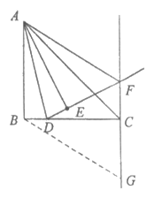
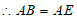 ,∠ABC=∠AED=90°,∠BAD=∠EAD 5分
,∠ABC=∠AED=90°,∠BAD=∠EAD 5分
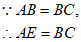
∴Rt△AEF≌Rt△BCG(HL) 6分
∴∠EAF=∠CBG
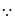 ∠BCG=90°,
∠BCG=90°,
∴∠BGC+∠CBG=90°
∴∠BAF+∠EAF=90°
∴∠BAD+∠EAD+∠EAF+∠EAF=90°
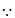 ∠BAD=∠EAD
∠BAD=∠EAD
∴∠EAD+∠EAF=45°
即∠DAF=45°。 7分
28.(1)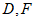 ; 2分
; 2分
(2)①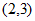 ; 3分
; 3分
②当直线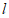 经过点
经过点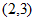 时,
时,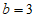 ,
,
当直线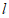 经过点
经过点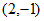 时,
时,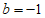 ,
,
所以若直线 上存在点A的”2-距点”,
上存在点A的”2-距点”,
图形 5分
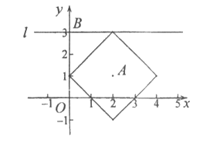
则b的取值范围是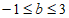 。 6分
。 6分

 工序
工序