一、选择题共5小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 设向量a,b满足|a|=2,|b|=1,<a,b>=60°,则|a+2b|=( )
A. 2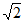 B. 2
B. 2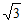 C.
C. 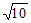 D. 12
D. 12
2. 下列函数中,最小正周期为1的奇函数为( )
A. 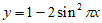 B.
B.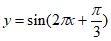
C. 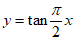 D.
D.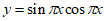
3. 要得到函数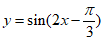 的图像,只需将函数
的图像,只需将函数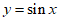 的图像上所有的点( )
的图像上所有的点( )
A. 先向右平移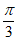 个单位长度,再将横坐标伸长到原来的2倍,纵坐标不变
个单位长度,再将横坐标伸长到原来的2倍,纵坐标不变
B. 先向右平移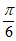 个单位长度,再将横坐标缩短为原来的
个单位长度,再将横坐标缩短为原来的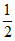 倍,纵坐标不变
倍,纵坐标不变
C. 先将横坐标缩短为原来的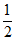 倍,纵坐标不变,再向右平移
倍,纵坐标不变,再向右平移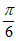 个单位长度
个单位长度
D. 先将横坐标伸长为原来的2倍,纵坐标不变,再向右平移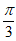 个单位长度
个单位长度
4. 在△ABC中,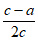 =sin
=sin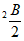 (a,b,c为角A,B,C三对边),则△ABC的形状为( )
(a,b,c为角A,B,C三对边),则△ABC的形状为( )
A. 直角三角形 B. 等边三角形
C. 等腰三角形或直角三角形 D. 等腰直角三角形
5. 在正方体AC1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F与平面D1AE的垂线垂直,如图所示,下列说法不正确的是( )
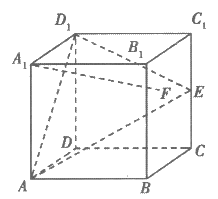
A. 点F的轨迹是一条线段 B. A1F与BE是异面直线
C. A1F与D1E不可能平行 D. 三棱锥F-ABD1的体积为定值
二、填空题共10小题。
6. 已知角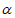 的终边经过点P(-3,4),则sin
的终边经过点P(-3,4),则sin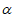 =____________。
=____________。
7. 已知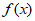 =
=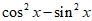 ,则
,则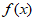 的最小正周期是____________。
的最小正周期是____________。
8. 已知点A(1,2),B(2,3),C(-2,5),则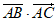 =___________。
=___________。
9. 在△ABC中,a=2,b=2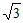 ,A=30°,则角B=___________。
,A=30°,则角B=___________。
10. 设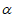 、
、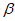 是两个不同的平面,l是直线且l
是两个不同的平面,l是直线且l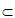
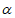 ,则”l⊥
,则”l⊥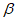 “是”
“是”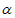 ⊥
⊥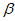 “的_________条件(参考选项:充分不必要,必要不充分,充分必要,既不充分也不必要)。
“的_________条件(参考选项:充分不必要,必要不充分,充分必要,既不充分也不必要)。
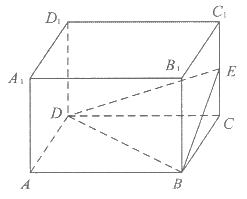
11. 如图,长方体ABCD-A1B1C1D1的体积为60,E为CC1的中点,则三棱锥E-BCD的体积是___________。
12. 若在△ABC中,A=60°,b=1,S△ABC=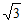 ,则
,则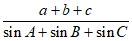 =___________。
=___________。
13. 已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上。若AB=3,AC=4,AB⊥AC,AA1=12,则球O的表面积为___________。
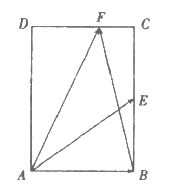
14. 如图,在矩形ABCD中,AB=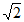 ,BC=2,点E为BC的中点,点F在边CD上,若
,BC=2,点E为BC的中点,点F在边CD上,若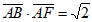 ,则
,则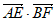 的值是___________。
的值是___________。
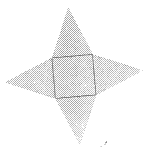
15. 如图,以正方形的各边为底可向外作四个腰长为l的等腰三角形,则阴影部分面积的最大值是___________。
三、解答题共5小题。解答应写出文字说明、演算步骤或证明过程。
16. 已知函数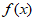 =2 sin(2x-
=2 sin(2x-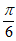 )。
)。
(1)求函数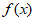 的对称轴;
的对称轴;
(2)当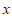 ∈[0,
∈[0,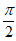 ]时,求函数
]时,求函数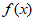 的最大值与最小值。
的最大值与最小值。
17. 在△ABC中,a,b,c分别是角A,B,C的对边,且c=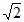 ,A=105°,C=30°。求:
,A=105°,C=30°。求:
(1)b的值;
(2)△ABC的面积。
18. 如图,三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,C1B1中点。
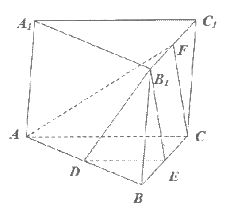
(1)求证:AC∥平面B1DE;
(2)求证:平面ACF∥平面B1DE。
19. 已知△ABC的角A,B,C所对的边分别为a,b,c且acosC+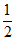 c=b。
c=b。
(1)求角A的大小;
(2)若a=1,求△ABC周长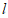 的最大值。
的最大值。
20. 如图1,在△ABC中,D,E分别为AB,AC的中点,O为DE的中点,AB=AC=2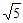 ,BC=4。将△ADE沿DE折起到△A1DE的位置,使得平面A1DE⊥平面BCED,F为A1C的中点,如图2。
,BC=4。将△ADE沿DE折起到△A1DE的位置,使得平面A1DE⊥平面BCED,F为A1C的中点,如图2。
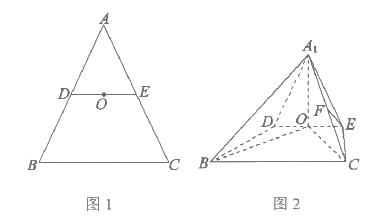
(1)求证:EF∥平面A1BD;
(2)求证:平面A1OB⊥平面A1OC;
(3)线段OC上是否存在点G,使得OC⊥平面EFG?说明理由。
参考答案
1. B
2. D
3. C
4. A
5. C
6. 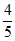 。
。
7. 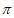 。
。
8. 0。
9. 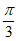 或
或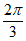 。
。
10. 充分不必要。
11. 5。
12. 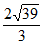 。
。
13. 169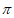 。
。
14. 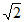 。
。
15. 2+2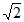 。
。
16. 
(1)令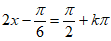 ,k∈Z,得2x=
,k∈Z,得2x=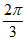 +
+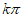 ,k∈Z,故
,k∈Z,故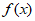 图像的对称轴为
图像的对称轴为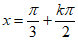 ,k∈Z。
,k∈Z。
(2)当x∈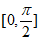 时,2x-
时,2x-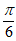
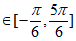 ,由y=
,由y=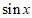 性质知:当
性质知:当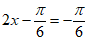 ,即x=0时,min{f(x)}=f(0)=-1;当2x-
,即x=0时,min{f(x)}=f(0)=-1;当2x-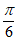 =
=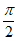 ,即x=
,即x=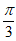 时,max{f(x)}=f(
时,max{f(x)}=f(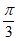 )=2。
)=2。
17. (1)2;(2)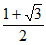 。
。
18. (1)在△ABC中,D,E分别为棱AB,BC中点,所以DE∥AC。因为DE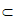 平面B1DE,AC
平面B1DE,AC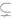 平面B1DE,所以AC∥平面B1DE。
平面B1DE,所以AC∥平面B1DE。
(2)在三棱柱ABC-A1B1C1中,BC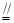 B1C1,因为E,F分别为BC,B1C1中点,所以CE
B1C1,因为E,F分别为BC,B1C1中点,所以CE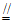 B1F,所以B1ECF是平行四边形。所以FC∥B1E,因为FC
B1F,所以B1ECF是平行四边形。所以FC∥B1E,因为FC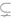 平面B1ED,B1E
平面B1ED,B1E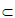 平面B1ED,所以FC∥平面B1DE,又因为AC∥平面B1DE,AC
平面B1ED,所以FC∥平面B1DE,又因为AC∥平面B1DE,AC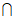 CF=C,所以平面ACF∥平面B1DE,所以AF∥平面B1DE。
CF=C,所以平面ACF∥平面B1DE,所以AF∥平面B1DE。
19. (1)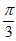 ;(2)3。
;(2)3。
(1)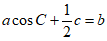 ,所以
,所以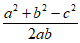 +
+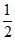 c=b,所以
c=b,所以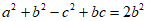 ,所以
,所以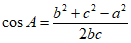 =
=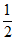 。因为A∈(0,
。因为A∈(0,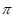 ),所以A=
),所以A=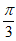 ,所以B+C=
,所以B+C=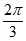 ;
;
(2)a=1,由正弦定理得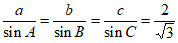 。所以
。所以
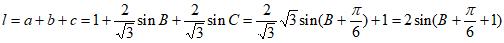 ,其中
,其中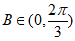 。所以当
。所以当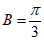 时,
时, 的最大值为3。
的最大值为3。
20. (1)取线段A1B的中点H,连接HD,HF。
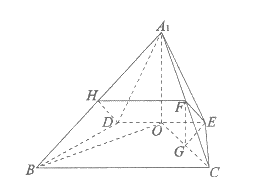
因为在△ABC中,D,E分别为AB,AC的中点,
所以DE∥BC,DE=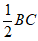 。
。
因为H,F分别为A1B,A1C的中点,
所以HF∥BC,HF=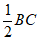 ,
,
所以HF∥DE,HF=DE,
所以四边形DEFH为平行四边形,
所以EF∥HD。
因为EF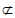 平面A1BD,HD
平面A1BD,HD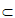 平面A1BD,
平面A1BD,
所以EF∥平面A1BD。
(2)因为在△ABC中,D,E分别为AB,AC的中点,
所以AD=AE。
所以A1D=A1E,又O为DE的中点,
所以A1O⊥DE。
因为平面A1DE⊥平面BCED,且A1O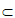 平面A1DE,
平面A1DE,
所以A1O⊥平面BCED,
所以CO⊥A1O。
在△OBC中,BC=4,易知OB=OC=2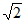 ,
,
所以CO⊥BO。
所以CO⊥平面A1OB,
所以平面A1OB⊥平面A1OC。
(3)线段OC上不存在点G,使得OC⊥平面EFG。
否则,假设线段OC上存在点G,使得OC⊥平面EFG,
连接GE,GF,
则必有OC⊥GF,且OC⊥GE。
在Rt△A1OC中,由F为A1C的中点,OC⊥GF,
得G为OC的中点。
在△EOC中,因为OC⊥GE,
所以EO=EC,
这显然与EO=1,EC=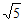 矛盾!
矛盾!
所以线段OC上不存在点G,使得OC⊥平面EFG。
