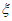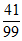一、选择题共10小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 已知集合A={x|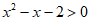 },则
},则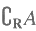 =( )
=( )
A. {x|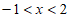 } B. {x|
} B. {x|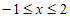 }
}
C. {x|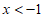 }
}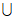 {x|
{x|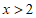 } D. {x|
} D. {x|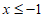 }
}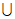 {x|
{x|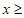 2}
2}
2. a=60.7,b=0.76,c=log0.7 6的大小顺序是( )
A. b<c<a B. b<a<c C. c<a<b D. c<b<a
3. 设x∈R,则”0<x<5″是”|x-1|<l”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
4. 某班由24名男生和16名女生组成,现按分层抽样的方法选取10名同学参加志愿者服务,某男同学必须参加,则志愿者人员组成的不同方法种数为( )
A. 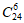
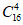 B.
B. 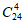
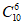 C.
C. 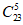
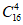 D.
D.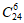
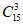
5. 若对于任意实数x,有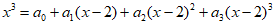 ,则a2的值为( )
,则a2的值为( )
A. 3 B. 6 C. 9 D. 12
6. 下列函数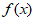 图象中,满足
图象中,满足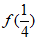 >
>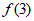 >
>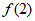 的只可能是( )
的只可能是( )
A. 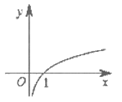 B.
B.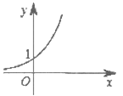
C. 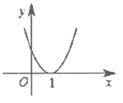 D.
D.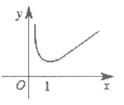
7. 如图所示,1,2,3表示三个开关,若在某段时间内它们每个正常工作的概率都是0.9,那么此系统的可靠性是( )
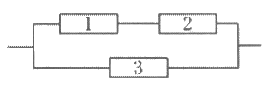
A. 0.999 B. 0.981 C. 0.980 D. 0.729
8. 设函数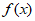 (x∈R)为奇函数,
(x∈R)为奇函数,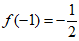 ,
,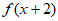 =
=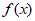 +
+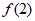 ,则
,则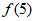 =( )
=( )
A. 0 B. 1 C. 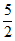 D. 5
D. 5
9. 已知函数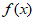 =(
=(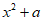 )
)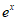 有最小值,则函数
有最小值,则函数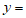
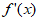 的零点个数为( )
的零点个数为( )
A. 0 B. 1 C. 2 D. 与a有关
10. 设直线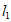 ,
,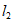 分别是函数
分别是函数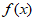 =
=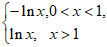 图像上点P1,P2处的切线,
图像上点P1,P2处的切线,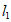 与
与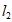 垂直相交于点P,且
垂直相交于点P,且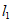 ,
,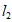 分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
分别与y轴相交于点A,B,则△PAB的面积的取值范围是( )
A. (0,1) B. (0,2) C. (0,+∞) D. (1,+∞)
二、填空题共5小题。
11. 函数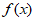 =
=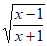 的定义域是__________。
的定义域是__________。
12. 函数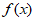 =lnx+x+
=lnx+x+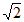 的零点个数是__________。
的零点个数是__________。
13. 已知log5
x+log5
y=2,则x+4y的最小值为__________。
14. 设函数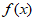 =x|
=x|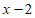 |,则
|,则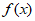 的极小值是__________。
的极小值是__________。
15. 定义在R上的函数 满足
满足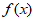 =
=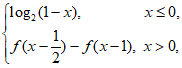 则
则 的值是___________。
的值是___________。
三、解答题共5小题。解答应写出文字说明、演算步骤或证明过程。
16. 设A={x∈R| y=log2
x},B={x∈R|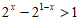 },则求A
},则求A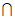 B。
B。
17. 已知关于x的不等式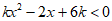 (k≠0)。
(k≠0)。
(1)若不等式的解集是{x|x>-2或x<-3},求k的值;
(2)若不等式的解集为R,求k的取值范围。
18. 已知函数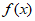 =
=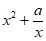 (x≠0,常数a∈R)。
(x≠0,常数a∈R)。
(1)讨论函数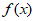 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)若函数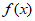 在[2,+∞)上为增函数,求a的取值范围。
在[2,+∞)上为增函数,求a的取值范围。
19.某中学参加一次社会公益活动(以下简称活动)。该校合唱团共有100名学生,他们参加活动的次数统计如图所示。
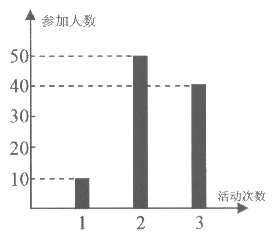
(1)求合唱团学生参加活动的人均次数;
(2)从合唱团中任意选两名学生,求他们参加活动次数恰好相等的概率;
(3)从合唱团中任选两名学生,用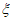 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量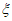 的分布列及数学期望E
的分布列及数学期望E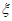 。
。
20. 对于函数y=H(x),若在定义域内存在x0,使得x0·H(x0)=1,则称x0为函数H(x)的”倒数点”。已知函数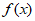 =lnx,g(x)=
=lnx,g(x)=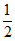 (x+1)2-1。
(x+1)2-1。
(1)求证:函数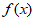 有”倒数点”,并讨论函数
有”倒数点”,并讨论函数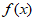 的”倒数点”的个数;
的”倒数点”的个数;
(2)若当x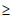 l时,不等式x
l时,不等式x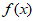 ≤m[g(x)-x]恒成立,试求实数m的取值范围。
≤m[g(x)-x]恒成立,试求实数m的取值范围。
参考答案
1. B 2. D 3. B
4. C 5. B 6. D
7. B 8. C 9. C
10. A
设P1(x1,lnx1),P2(x2,-lnx2)(不妨设x1>1,0<x2<1),
则由导数的几何意义易得切线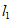 ,
,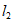 的斜率分别是
的斜率分别是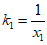 ,
,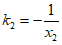 。
。
由已知得k1k2=-l,
所以x1x2=1,
所以x2=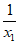 。
。
所以切线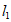 的方程为
的方程为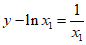 (x–x1),
(x–x1),
切线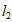 的方程为
的方程为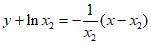 ,
,
即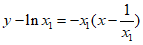 。
。
分别令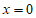 得
得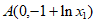 ,
,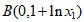 。
。
又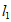 与
与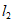 的交点为P(
的交点为P(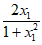 ,
,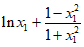 )。
)。
因为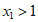 ,
,
所以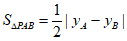 ·
·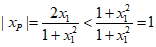 ,
,
所以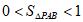 。
。
11. (-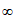 ,-1)
,-1)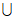 [1,+
[1,+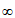 ]。
]。
12. 1。
13. 20。
14. 0。
15. 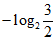 。
。
16. A=(0,+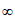 ),B=(1,+
),B=(1,+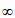 ),A
),A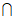 B=(1,+
B=(1,+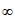 )。
)。
17. (1)因为不等式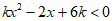 (k≠0)的解集是{x|x>-2或x<-3},
(k≠0)的解集是{x|x>-2或x<-3},
所以方程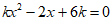 的两根为-3和-2,且k<0。
的两根为-3和-2,且k<0。
由根与系数的关系得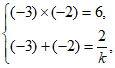
所以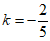 。
。
(2)因为不等式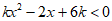 (k≠0)的解集为R,
(k≠0)的解集为R,
所以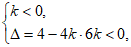 解得
解得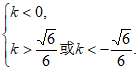
故k的取值范围是(-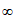 ,-
,- )。
)。
18. (1)当a=0时,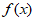 是偶函数;当a≠0时,
是偶函数;当a≠0时,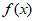 既不是奇函数,又不是偶函数。
既不是奇函数,又不是偶函数。
(2)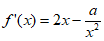 在[2,+
在[2,+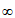 )上为非负,即
)上为非负,即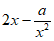 ≥0,
≥0,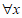 ≥2,a≤2
≥2,a≤2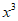 在[2,+
在[2,+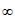 )上恒成立,而y=2
)上恒成立,而y=2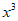 在[2,+
在[2,+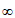 )上的最小值为16,所以a的取值范围是(-
)上的最小值为16,所以a的取值范围是(-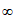 ,16]。
,16]。
19.
由图可知,参加活动1次,2次和3次的学生人数分别为10,50和40。
(1)该合唱团学生参加活动的人均次数为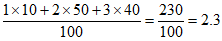 ;
;
(2)从合唱团中任选两名学生,他们参加活动次数恰好相等的概率为
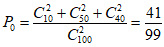 ;
;
(3)从合唱团中任选两名学生,记”这两人中一人参加l次活动,另一人参加2次活动”为事件A,”这两人中一人参加2次活动,另一人参加3次活动”为事件B,”这两人中一人参加1次活动,另一人参加3次活动”为事件C。易知
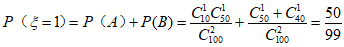 ;
;
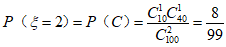 ;
;
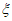 的分布列:
的分布列:
| 0 | 1 | 2 |
P |
|
|
|
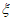 的数学期望:E
的数学期望:E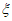 =0×
=0×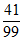 +1×
+1×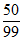 +2×
+2×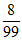 =
=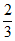 。
。
20. (1)设h(x)=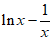 (x>0),则
(x>0),则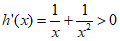 (x>0),所以h(x)在(0,+
(x>0),所以h(x)在(0,+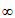 )为单调递增函数。而h(1)<0,h(e)>0所以函数h(x)有零点且只有一个零点。所以函数
)为单调递增函数。而h(1)<0,h(e)>0所以函数h(x)有零点且只有一个零点。所以函数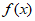 有且只有一个”倒数点”。
有且只有一个”倒数点”。
(2)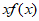 ≤m[g(x)-x]等价于2x·lnx≤m(x2-1),
≤m[g(x)-x]等价于2x·lnx≤m(x2-1),
设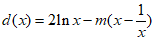 ,x≥l,
,x≥l,
则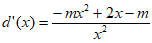 ,x≥l,
,x≥l,
易知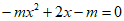 的判别式为
的判别式为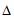 =4-4
=4-4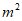 。
。
①当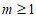 时,
时,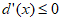 ,
,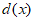 在[1,+
在[1,+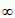 )上单调递减,
)上单调递减,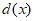 ≤d(1)=0,符合题意;
≤d(1)=0,符合题意;
②当0<m<1时,方程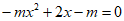 有两个正根且0<x1<l< x2,则函数
有两个正根且0<x1<l< x2,则函数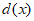 在(1,x2)上单调递增,此时d(x)>d(1)=0,不合题意;
在(1,x2)上单调递增,此时d(x)>d(1)=0,不合题意;
③当m=0时,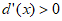 ,d(x)在(1,+
,d(x)在(1,+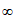 )上单调递增,此时
)上单调递增,此时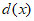 >d(1)=0,不合题意;
>d(1)=0,不合题意;
④当-l<m<0时,方程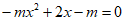 有两个负根,
有两个负根,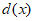 在(1,+
在(1,+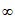 )上单调递增,此时
)上单调递增,此时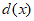 >d(1)=0,不合题意;
>d(1)=0,不合题意;
⑤当m≤-l时,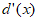 ≥0,d(x)在(1,+
≥0,d(x)在(1,+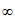 )上单调递增,此时d(x)>d(1)=0,不合题意。
)上单调递增,此时d(x)>d(1)=0,不合题意。
综上,实数m的取值范围是[1,+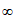 )。
)。