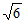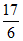考试时间:100分钟 满分:120分
一、选择题(每题2分,共20分)
1. 平面直角坐标系中,点(3,-2)在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2. 若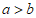 ,则下列不等式中不正确的是( )
,则下列不等式中不正确的是( )
A. 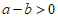 B.
B. 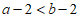 C.
C. 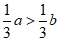 D.
D.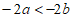
3. 北京2022年冬奥会会徽是以汉字“冬“为灵感来源设计的。在下面右侧的四个图中,能由图1经过平移得到的是(
)

图1




A B C D
4. 81的算术平方根是( )
A. 9 B. 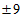 C. 3 D.
C. 3 D.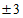
5. 下列调查中,调查方式选择合理的是( )
A. 为了了解某一批灯泡的寿命,选择全面调查
B. 为了了解某年北京的空气质量,选择抽样调查
C. 为了了解神舟飞船的设备零件的质量情况,选择抽样调查
D. 为了了解一批袋装食品是否含有防腐剂,选择全面调查
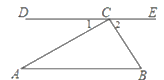
6. 如图,在△ABC中,∠ACB=90°,CD//AB,∠ACD=36°那么∠B的度数为(
)
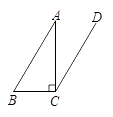
A. 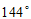 B.
B. 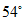 C.
C. 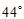 D.
D.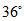
7. 下列各数中无理数有( )
3. 141,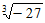 ,
,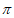 ,
,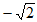 ,0,
,0,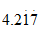 ,0. 1010010001
,0. 1010010001
A. 5个 B. 4个 C. 3个 D. 2个
8. 如果点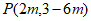 在第四象限,那么
在第四象限,那么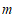 的取值范围是( )
的取值范围是( )
A. 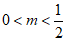 B.
B. 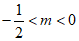 C.
C. 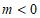 D.
D.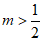
9. 如图①,一张四边形纸片ABCD,∠A=50°,∠C=150°。若将其按照图②所示方式折叠后,恰好MD′∥AB,ND′∥BC,则∠D的度数为 ( )
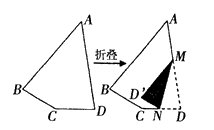
图① 图②
A. 70° B. 75° C. 80° D. 85°
10. 如图,三个天平的托盘中形状相同的物体质量相等。图①②所示的两个天平处于平衡状态,要使第3个天平也保持平衡,则需在它的右盘中放置( )个球。

图① 图② 图③
A. 5 B. 6 C. 7 D. 8
二、填空题(11至17题每小题2分,18题4分,共18分)
11. –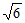 的相反数是______。
的相反数是______。
12. 在平面直角坐标系内,把点P(6,3)先向左平移2个单位长度,再向上平移4个单位长度后得到的点的坐标是______。
13. 若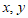 为实数,且
为实数,且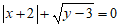 ,则
,则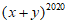 的值为_____________。
的值为_____________。
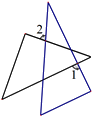
14. 一副三角板如下图所示放置,若∠1=90°,则∠2=______°。
15. 若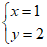 是方程
是方程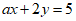 的一个解,则a的值为_________________________。
的一个解,则a的值为_________________________。
16. 已知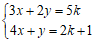 ,且y-x<2,则
,且y-x<2,则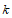 的取值范围是______。
的取值范围是______。
17. 在实数范围内规定新运算“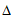 “,其规则是:
“,其规则是: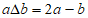 ,已知不等式
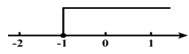
,已知不等式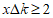 的解集在数轴上如图表示,则k的值是_____________________________________。
的解集在数轴上如图表示,则k的值是_____________________________________。
18. 阅读下面求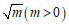 近似值的方法,回答问题:
近似值的方法,回答问题:
①任取正数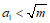 ;
;
②令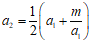 ,则
,则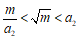 ;
;
③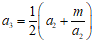 ,则
,则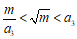 ;
;
……以此类推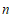 次,得到
次,得到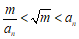 。
。
其中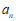 称为
称为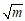 的
的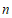 阶过剩近似值,
阶过剩近似值,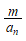 称为
称为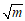 的
的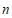 阶不足近似值。
阶不足近似值。
仿照上述方法,求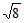 的近似值。
的近似值。
①取正数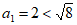 。
。
②于是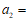 _____________________________________;
_____________________________________;
③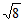 的
的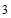 阶过剩近似值
阶过剩近似值 是_____________________________________。
是_____________________________________。
三、解答题(10大题,共62分)
19. (5分)计算: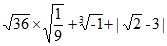
20. (5分)解方程组: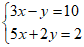
21. (5分)解不等式:2x+2≥3x﹣1,并把它的解集在数轴上表示出来。
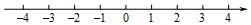
22. (5分)解不等式组: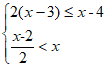 并求整数解。
并求整数解。
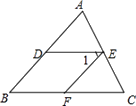
23. (6分)如图,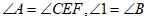 ,求证:
,求证: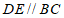 。
。
24. (6分)某校为了解学生的课外阅读情况,对部分学生进行了调查,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制如下两幅不完整的统计图。
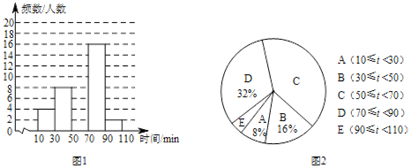
请你根据以上信息解答下列问题:
(1)本次调查活动的样本容量是_______________________。
(2)图2中E的圆心角度数为_____________度,并补全图1的频数分布直方图。
(3)该校有800名学生,估计该校学生平均每天的课外阅读时间不少于70min的人数。
25. (6分)如图,在直角坐标平面内,点A的坐标是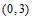 ,点B的坐标是
,点B的坐标是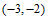
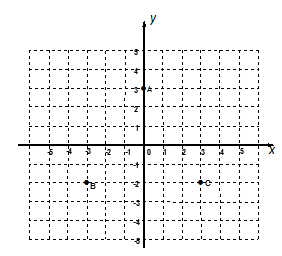
(1)图中点C关于x轴对称的点D的坐标是______。
(2)如果将点B沿着与y轴平行的方向向上平移5个单位得到点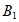 ,那么
,那么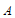 、
、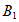 两点之间的距离是______。
两点之间的距离是______。
(3)求三角形ACD的面积。
26. (8分)某学校为了丰富学生的大课间活动,准备购进一批跳绳,已知2根短绳和1根长绳共需35元,1根短绳和2根长绳共需40元。
(1)求每根短绳和每根长绳的售价各是多少元?
(2)学校准备购进这两种跳绳共40根,并且短绳的数量不超过长绳数量的2倍,总费用不超过500元,请设计出最省钱的购买方案,并说明理由。
27. (8分)如图①,已知任意三角形ABC,过点C作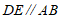 。
。
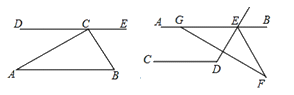
(1)如图①,求证:三角形ABC的三个内角(即 ,
, ,
, )之和等于
)之和等于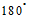 ;
;
(2)如图②,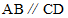 ,
,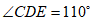 ,GF交
,GF交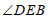 的平分线EF于点F,且
的平分线EF于点F,且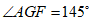 ,结合(1)中的结论,求
,结合(1)中的结论,求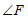 的度数。
的度数。
28. (8分)在平面直角坐标系中,若P、Q两点的坐标分别为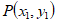 和
和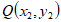 ,则定义
,则定义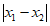 和
和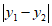 中较小的一个(若它们相等,则取其中任意一个)为P、Q两点的”最佳距离”,记为
中较小的一个(若它们相等,则取其中任意一个)为P、Q两点的”最佳距离”,记为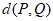 。例如:
。例如: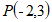 ,
,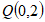 ,
,
因为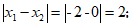
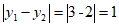 ,而2>1,所以
,而2>1,所以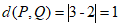
(1)请直接写出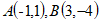 的”最佳距离”
的”最佳距离”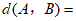 ____;
____;
(2)点D是坐标轴上的一点,它与点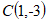 的”最佳距离”
的”最佳距离”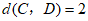 ,请写出点D的坐标_________________________________;
,请写出点D的坐标_________________________________;
(3)若点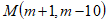 同时满足以下条件:
同时满足以下条件:
(a)点M在第四象限;
(b)点M与点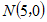 的”最佳距离”
的”最佳距离”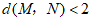 ;
;
(c)∠MON>45°(O为坐标原点)
请写出满足条件的整点(横纵坐标都为整数的点)M的坐标___________________。
附加题
本大题共5道小题,每题4分,共20分。请将你的答案填在表格中相应的位置。
1.
下列运算中正确的是( )
A. 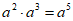 B.
B.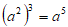
C. 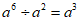 D.
D.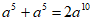
2.
已知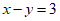 ,
,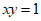 ,则
,则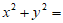 ( )
( )
A. 5 B. 7 C. 9 D. 11
3. 如图,根据计算长方形ABCD的面积,可以说明下列哪个等式成立( )
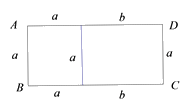
A. 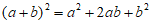
B. 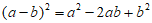
C. 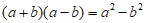
D. 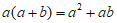
4.
要使分式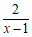 有意义,则x的取值范围是________。
有意义,则x的取值范围是________。
5.
分解因式: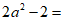 ____________。
____________。
参考答案
一、选择题:本大题共10小题,每题2分,共20分。
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
答案 | D | B | B | A | B | B | D | D | C | C |
二、填空题:本大题共8小题,每空2分,共18分。
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| (4,7) | 1 | 75 | 1 | k<1 | -4 | 3, |
三、解答题:本大题共10小题,共62分。
19.(本题5分)
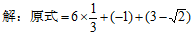 …3分
…3分
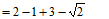 …4分
…4分
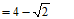 …5分
…5分
20.(本题5分)
解:①×2: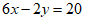 ③
③
②+③: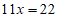
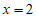 2分
2分
把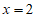 代入①,得
代入①,得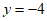 , … 4分
, … 4分
∴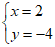 5分
5分
21. (本题5分)
解: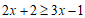
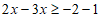 2分
2分
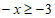 3分
3分
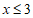 4分
4分
 5分
5分
22.(本题5分)
解: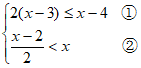
解不等式①,得x≤2,.. .. .. .. .. .. .. .. .. .. .. .. .. .. 1分
解不等式②,得x>-2,.. .. .. .. .. .. .. .. .. .. .. … .. 2分
不等式组的解集是-2<x≤2,.. .. .. .. .. .. .. .. .. . .. 3分
不等式组的正整数解是-1,0,1,2.. .. .. .. … .. 5分
23. (本题6分)
证明: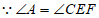
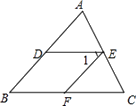
 . .. .. .. .. .. .. .. .. .. .. .. 2分
. .. .. .. .. .. .. .. .. .. .. .. 2分
 . .. .. .. .. .. .. .. .. .. .. .. .. .. 4分
. .. .. .. .. .. .. .. .. .. .. .. .. .. 4分
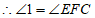
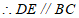 . .. .. .. .. .. .. .. .. .. .. .. .. .. . 6分
. .. .. .. .. .. .. .. .. .. .. .. .. .. . 6分
24. (本题6分)
(1)50 .. .. .. .. .. .. .. .. .. .. .. .. .. . 2分
(2)14. 4 图略 .. .. .. .. .. .. .. .. .. 4分
(3)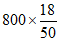 =288 . .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 6分
=288 . .. .. .. .. .. .. .. .. .. .. .. .. .. .. .. 6分
25. (本题6分)(1)(3,2), 2分
(2)3 4分
(3), …6分
26. (本题8分)
(1)解:设每根短绳的售价为元,每根长绳的售价为元, ……1分
则有 2分
解得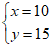 … ……3分
… ……3分
答:每根短绳的售价为10元,每根长绳的售价为15元. 4分
(2)解:设购买短绳根,长绳根 ……5分
则有 …6分
解集为 ……7分
可取20,21,22,23,24,25,26,且短绳比长绳便宜
答:买短绳26根,长绳14根时,最省钱。 …8分
27. (本题8分)
解:(1)如图所示,在△ABC中,∵DE∥AB,
∴∠B=∠2,∠C=∠1(两直线平行,内错角相等). …2分
∵∠1+∠BCA+∠2=180°
∴∠A+∠B+∠C=180°
即三角形的内角和为180° …4分
(2)∵AB∥CD,∠CDE=110°,
∴∠DEB=∠CDE=110°,∠AED=180°-∠CDE=70°, 5分
∵GF交∠DEB的平分线EF于点F,
∴∠DEF= ∠DEB=55°, …6分
∠DEB=55°, …6分
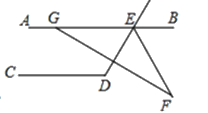
∴∠AEF=∠AED+∠DEF=125°,
∵∠AGF=145°,∠AGF+∠EGF=180°,∠EGF+∠AEF+∠F=180°
∴∠AGF=∠AEF+∠F,
∴∠F=145°-125°=20°。 …8分
28. (本题8分)
(1)4; ……2分
(2)(3,0)(-1,0); ……4分
(3)(4,-7)(5,-6) …8分
附加题
本大题共5道小题,每题4分,共20分。请将你的答案填在表格中相应的位置。
题号 | 1 | 2 | 3 | 4 | 5 |
答案 | A | D | D | x≠1 | 2(a-1)(a+1) |