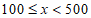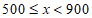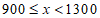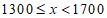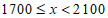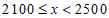考试时间:100分钟 满分:100分
一、选择题共10小题,每题2分。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 9的算术平方根是( )
A. -3 B. 3 C. 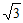 D. ±3
D. ±3
2. 已知a>b,下列不等式中,不正确的是( )
A. 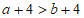 B.
B.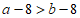
C. 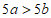 D.
D.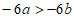
3. 下列运算正确的是( )
A. 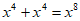 B.
B.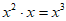
C. 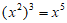 D.
D.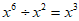
4. 若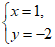 是关于
是关于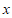 和
和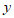 的二元一次方程
的二元一次方程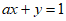 的解,则a的值等于( )
的解,则a的值等于( )
A. 3 B. 1 C. -1 D. -3
5. 下列调查方式,你认为最合适的是( )
A. 疫情防控阶段进出某小区人员的体温检测,采用抽样调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C. 了解2020年五一期间圆明园每天的客流量,采用全面调查的方式
D. 检测一批手持测温仪的使用寿命,采用全面调查的方式
6. 若把不等式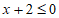 的解集在数轴上表示出来,则正确的是( )
的解集在数轴上表示出来,则正确的是( )
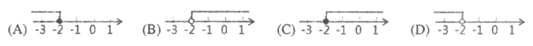
7. 下列各式由左边到右边的变形中,是因式分解的是( )
A. 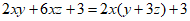 B.
B.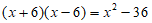
C. 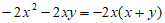 D.
D.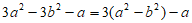
8. 已知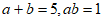 ,则
,则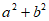 的值为( )
的值为( )
A. 6 B. 23 C. 24 D. 27
9. 如图,已知长方形纸片的一条边经过直角三角形纸片的直角顶点,若矩形纸片的一组对边与直角三角形的两条直角边相交成∠1,∠2. 则∠1与∠2的关系为( )
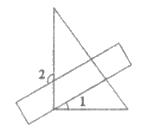
A. ∠1+∠2=180° B. ∠2=4∠1 C. ∠2=∠1+90° D. ∠1+∠2=150°
10. 已知关于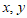 的二元一次方程
的二元一次方程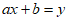 ,下表列出了当x分别取值时对应的y的值,则关于x的不等式
,下表列出了当x分别取值时对应的y的值,则关于x的不等式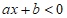 的解集为( )
的解集为( )
| … | -2 | -1 | 0 | 1 | 2 | 3 | … |
| … | 3 | 2 | 1 | 0 | -1 | -2 | … |
A. 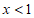 B.
B. 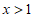 C.
C. 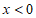 D.
D.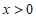
二、填空题共8小题,每题3分。
11. 若点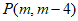 在平面直角坐标系的y轴上,则点P的坐标是__________。
在平面直角坐标系的y轴上,则点P的坐标是__________。
12. 比较大小: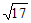 __________5。(填”>”,”=”,”<”)
__________5。(填”>”,”=”,”<”)
13. 将点A(-1,4)向上平移三个单位,得到点B,则B的坐标为____________。
14. 如图,直线AB,CD交于点O,OE⊥AB,若∠AOD=60°,则∠COE的度数为________度。
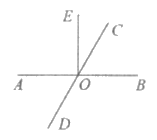
15. 若实数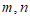 满足
满足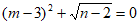 ,则
,则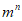 =_________。
=_________。
16. 如果关于x的不等式组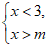 无解,那么m的取值范围是_____________。
无解,那么m的取值范围是_____________。
17. 若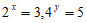 ,则
,则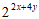 =____________。
=____________。
18. 2019年,部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,某国创新综合排名全球第13,创新效率排名全球第_________。
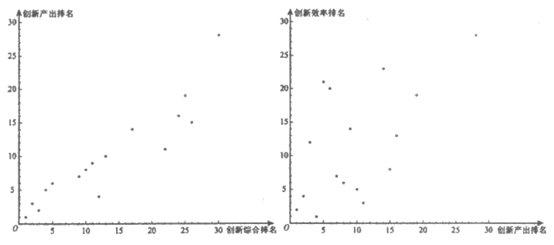
三、解答题共10小题。解答应写出文字说明、演算步骤或证明过程。
19. (4分)计算: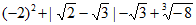 。
。
20. (4分)解方程组: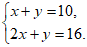
21. (4分)分解因式: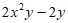 。
。
22. (6分)求不等式组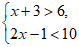 的整数解。
的整数解。
23. (6分)已知:如图,AD∥BC,∠B=∠D,求证:∠E=∠F。
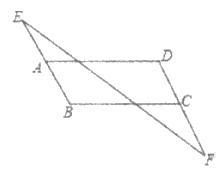
24. (6分)先化简,再求值: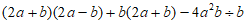 ,其中
,其中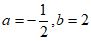 。
。
25. (8分)某汽车专卖店销售A,B两种型号的新能源汽车,上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元。
(1)求每辆A型车和B型车的售价各为多少万元;
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,则有哪几种购车方案?
26. (4分)致敬,最美逆行者!病毒虽无情,人间有大爱。2020年,在湖北省抗击新型冠状病毒的战”疫”中,全国(除湖北省外)共有30个省(区、市)及军队的医务人员在党中央全面部署下,白衣执甲,前赴后继支援湖北省抗击疫情,据国家卫健委的统计数据,截止3月1日,这30个省(区、市)累计派出医务人员总数多达38478人,其中派往湖北省除武汉外的其他地区的医务人员总数为7381人。
组别 | 医务人员数分组 | 频数 | 频率 |
1 |
| 3 | b |
2 |
| 10 | 0.33 |
3 |
| a | 0.33 |
4 |
| 4 | 0.14 |
5 |
| 2 | 0.07 |
6 |
| 1 | 0.03 |
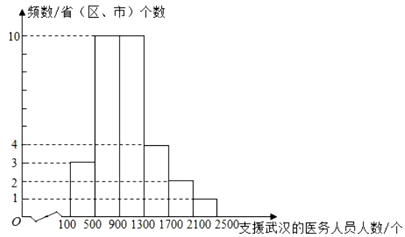
根据以上信息回答下列问题:
(1)频数分布表中的a=__________,b=___________;
(2)补全支援武汉的医务人员的频数分布直方图;
(3)这次支援湖北省抗疫中,全国30个省(区、市)派往武汉的医务人员总数大约____________万。(保留一位小数)
27. (7分)喜欢思考的小泽同学,设计了一种折叠纸条的游戏。
如图1,纸条的一组对边PN∥QM(纸条的长度视为可延伸),在PN,QM上分别找一点A,B,使得∠ABM=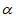 。
。
如图2,将纸条作第一次折叠,使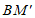 与BA在同一条直线上,折痕记为
与BA在同一条直线上,折痕记为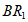 。
。
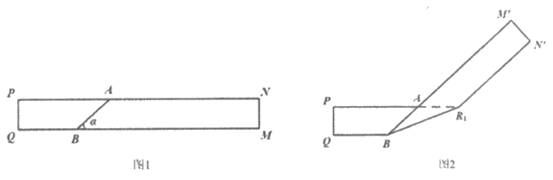
解决下面的问题:
(1)聪明的小白想计算当α=90°时,∠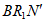 的度数,于是他将图2转化为下面的几何问题,请帮他补全问题并求解:
的度数,于是他将图2转化为下面的几何问题,请帮他补全问题并求解:
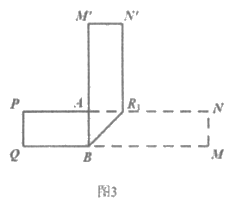
如图3,PN∥QM,A,B分别在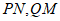 上,且∠ABM=90°,由折叠:
上,且∠ABM=90°,由折叠: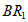 平分_________,
平分_________,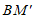 ∥
∥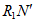 ,求∠
,求∠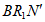 的度数。
的度数。
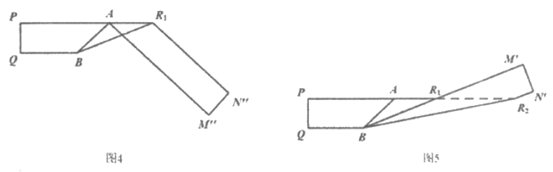
(2)聪颖的小桐提出了一个问题:按图2折叠后,不展开纸条,再沿AR1折叠纸条(如图4),是否有可能使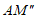 ⊥BR1?如果能,请直接写出此时
⊥BR1?如果能,请直接写出此时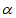 的度数;如果不能,请说明理由。
的度数;如果不能,请说明理由。
(3)笑笑看完此题后提出了一个问题:当0°<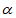 ≤90°时,将图2记为第一次折叠;将纸条展开,作第二次折叠,使
≤90°时,将图2记为第一次折叠;将纸条展开,作第二次折叠,使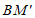 与BR1在同一条直线上,折痕记为BR2(如图5);将纸条展开,作第三次折叠,使
与BR1在同一条直线上,折痕记为BR2(如图5);将纸条展开,作第三次折叠,使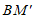 与BR2在同一条直线上,折痕记为BR3;…以此类推。
与BR2在同一条直线上,折痕记为BR3;…以此类推。
①第二次折叠时,∠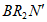 =_____________(用
=_____________(用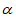 的式子表示);
的式子表示);
②第n次折叠时,∠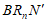 =____________(用
=____________(用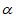 和n的式子表示)。
和n的式子表示)。
28.(7分)对于三个数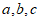 ,用
,用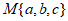 表示这三个数的平均数,用
表示这三个数的平均数,用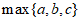 表示这个三个数中最大的数。例如:
表示这个三个数中最大的数。例如: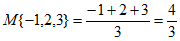 ,
,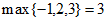 ,
,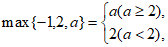
解决下列问题:(1)①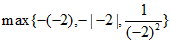 =____________。
=____________。
②如果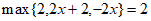 ,则x的取值范围为______________。
,则x的取值范围为______________。
(2)①如果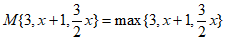 ,则x=____________。
,则x=____________。
②根据①,你发现了结论”如果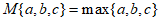 ,那么____________(填
,那么____________(填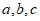 的大小关系)”。
的大小关系)”。
③运用②的结论,填空:
若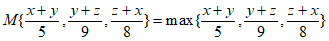 ,并且
,并且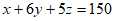 ,则
,则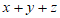 =_____________。
=_____________。
【试题答案】
1. B 2. D 3. B 4. A 5. C 6. A 7. C 8. B 9. C 10. B
11. 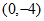 12. < 13.
12. < 13. 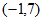 14. 30° 15. 9 16.
14. 30° 15. 9 16.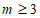
17. 225 18. 5 19. 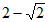 原式=
原式=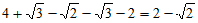 。
。
20. 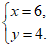
21. 原式=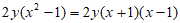 。
。
22. 4,5。
由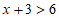 得
得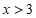 ,由
,由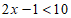 得
得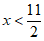 ,
,
所以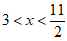 ,
,
原不等式组的整数解为4,5。
23. 因为AD∥BC,所以∠D=∠BCF,
又因为∠B=∠D,所以∠B=∠BCF,
所以BE∥DF,所以∠E=∠F。
24. 原式=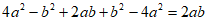 ,
,
当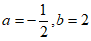 时,原式=-2。
时,原式=-2。
25. (1)设每辆A型车和B型车的售价分别是x万元、y万元。
则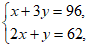 解得
解得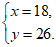
答:每辆A型车的售价为18万元,每辆B型车的售价为26万元。
(2)设购买A型车a辆,则购买B型车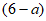 辆,则依题意得
辆,则依题意得
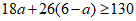 ,解得
,解得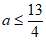 ,所以
,所以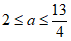 。
。
因为a是正整数,所以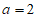 或
或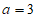 。
。
共有两种方案:
方案一:购买2辆A型车和4辆B型车;
方案二:购买3辆A型车和3辆B型车。
26. (1)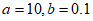 ;(2)略;(3)3.1。
;(2)略;(3)3.1。
27. (1)∠ABM,∠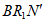 =135°;(2)
=135°;(2)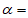 60°;(3)180°-
60°;(3)180°- ,180°-
,180°-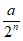 。
。
28. (1)①2
②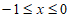
(2)①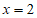
②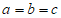
③33